Chapter: Mechanical : Finite Element Analysis : Applications in Heat Transfer & Fluid Mechanics
Application to Heat Transfer Two-Dimentional
APPLICATION TO HEAT TRANSFER TWO-DIMENTIONAL
1Strong Form for Two-Point Boundary Value Problems
The equations developed in this chapter for heat conduction, diffusion and elasticity problems are all of the following form:
Such one-dimensional problems are called two-point boundary value problems. gives the particular meanings of the above variables and parameters for several applications. The natural boundary conditions can also be generalized as (based on Becker et al. (1981))
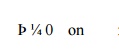
Equation is a natural boundary condition because the derivative of the solution appears in it. reduces to the standard natural boundary conditions considered in the previous sections when bðx Þ ¼ 0. Notice that the essential boundary condition can be recovered as a limiting case of when bðxÞ is a penalty parameter, i.e. a large number In this case, and Equation is called a generalized boundary condition.
An example of the above generalized boundary condition is an elastic bar with a spring attached as shown in In this case, bðlÞ ¼ k and reduces to
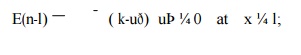
where ¼ k is the spring constant. If the spring stiffness is set to a very large value, the above boundary condition enforces ¼ u; if we let k ¼ 0, the above boundary condition corresponds to a prescribed traction boundary. In practice, such generalized boundary conditions are often used to model the influence of the surroundings. For example, if the bar is a simplified model of a building and its foundation, the spring can represent the stiffness of the soil.
2 Two-Point Boundary Value Problem With Generalized Boundary Conditions

An example of the generalized boundary for elasticity problem.
Another example of the application of this boundary condition is convective heat transfer, where energy is transferred between the surface of the wall and the surrounding medium. Suppose convective heat transfer occurs at x ¼ l. Let T ðlÞ be the wall temperature at x ¼ l and T be the temperature in the medium. Then the flux at the boundary x ¼ l is given by qð lÞ ¼ hðT ðlÞ T Þ, so bðlÞ ¼ h and the boundary condition is where h is convection coefficient, which has dimensions of W m 2 o C 1 . Note that when the convection coefficient is very large, the temperature T is immediately felt at x ¼ l and thus the essential boundary condition is again enforced as a limiting case of the natural boundary condition.
There are two approaches to deal with the boundary condition . We will call them the penalty and partition methods. In the penalty method, the essential boundary condition is enforced as a limiting case of the natural boundary condition by equating bðxÞ to a penalty parameter. The resulting strong form for the penalty method is given in.
General strong form for 1D problems-penalty method
þ f ¼ 0 on ;
In the partition approach, the total boundary is partitioned into the natural boundary, and the complementary essential boundary, The natural boundary condition has the generalized form defined by The resulting strong form for the partition method is summarized in.
3 Weak Form for Two-Point Boundary Value Problems
In this section, we will derive the general weak form for two-point boundary value problems. Both the penalty and partition methods described in will be considered. To obtain the general weak form for the penalty method, we multiply the two equations in the strong by the weight function and integrate over the domains over which they hold: the domain for the differential equation and the domain for the generalized boundary condition.
Related Topics