Chapter: Embedded Systems Design : Interfacing to the analogue world
Analogue to digital conversion techniques
Analogue to digital conversion
techniques
The basic principle behind analogue to digital conversion is simple and
straightforward: the analogue signal is sampled at a regular interval and each
sample is divided or quantised by a given value to determine the number of
given units of value that approximate to the analogue value. This number is the
digital equivalent of the analogue signal.
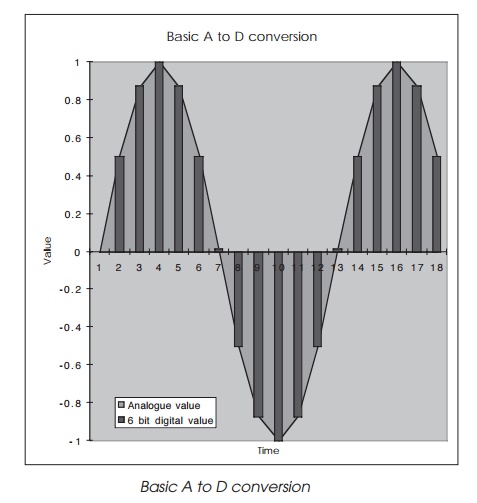
The combination graph shows the general principle. The grey curve
represents an analogue signal which, in this case, is a sine wave. For each
cycle of the sine wave, 13 digital samples are taken which encode the digital
representation of the signal.
Quantisation errors
Careful examination of the combination chart reveals that all is not
well. Note the samples at time points 7 and 13. These should be zero — however,
the conversion process does not convert them to zero but to a slightly higher
value. The other points show similar errors; this is the first type of error
that the conversion process can cause. These errors are known as quantisation
errors and are caused by the fact that the digital representation is step based
and consists of a selection from one of a fixed number of values. The analogue
signal has an infinite range of values and the difference between the digital
value the conver-sion process has selected and the analogue value is the
quantisation error.
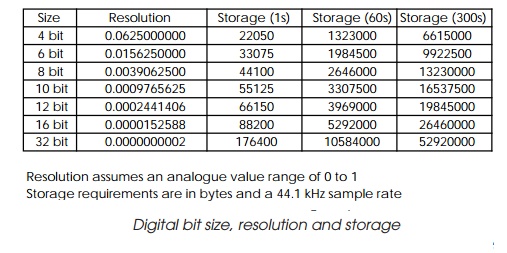
The size of the quantisation error is dependent on the number of bits
used to represent the analogue value. The table shows the resolution that can
be achieved for various digital sizes. As the table depicts, the larger the
digital representation, the finer the analogue resolution and therefore the
smaller the quantisation error and resultant distortion. However, the table
also shows the increase which occurs with the amount of storage needed. It
assumes a sample rate of 44.1 kHz, which is the same rate as used with an audio
CD. To store five minutes of 16 bit audio would take about 26 Mbytes of
storage. For a stereo signal, it would be twice this value.
Related Topics