Amplitude Modulation

AMPLITUDE MODULATION:

"Modulation is the process of superimposing a low frequency signal on a high frequency carrier signal."

OR

"The process of modulation can be defined as varying the RF carrier wave in accordance with the intelligence or information in a low frequency signal."

OR

"Modulation is defined as the precess by which some characteristics, usually amplitude, frequency or phase, of a carrier is varied in accordance with instantaneous value of some other voltage, called the modulating voltage."

^ü   Need For Modulation

1. If two musical programs were played at the same time within distance, it would be difficult for anyone to listen to one source and not hear the second source. Since all musical sounds have approximately the same frequency range, form about 50 Hz to 10KHz. If a desired program is shifted up to a band of frequencies between 100KHz and 110KHz, and the second program shifted up to the band between 120KHz and 130KHz, Then both programs gave still 10KHz bandwidth and the listener can (by band selection) retrieve the program of his own choice. The receiver would down shift only the selected band of frequencies to a suitable range of 50Hz to 10KHz.

2. A second more technical reason to shift the message signal to a higher frequency is related to antenna size. It is to be noted that the antenna size is inversely proportional to the frequency to be radiated. This is 75 meters at 1 MHz but at 15KHz it has increased to 5000 meters (or just over 16,000 feet) a vertical antenna of this size is impossible.

3. The third reason for modulating a high frequency carrier is that RF (radio frequency) energy will travel a great distance than the same amount of energy transmitted as sound power.

^ü   Types of Modulation

The carrier signal is a sine wave at the carrier frequency. Below equation shows that the sine wave has three characteristics that can be altered.

Instantaneous voltage (E) =E_c(max)Sin(2πf_ct + θ)

The term that may be varied are the carrier voltage Ec, the carrier frequency fc, and the carrier phase angle θ. So three forms of modulations are possible.

1.     Amplitude Modulation

Amplitude modulation is an increase or decrease of the carrier voltage (Ec), will all other factors remaining constant.

2.     Frequency Modulation

Frequency modulation is a change in the carrier frequency (fc) with all other factors remaining constant.

3.     Phase Modulation

Phase modulation is a change in the carrier phase angle (θ). The phase angle cannot change without also affecting a change in frequency. Therefore, phase modulation is in reality a second form of frequency modulation.

^ü EXPLAINATION OF AM:

The method of varying amplitude of a high frequency carrier wave in accordance with the information to be transmitted, keeping the frequency and phase of the carrier wave unchanged is called Amplitude Modulation. The information is considered as the modulating signal and it is superimposed on the carrier wave by applying both of them to the modulator. The detailed diagram showing the amplitude modulation process is given below.

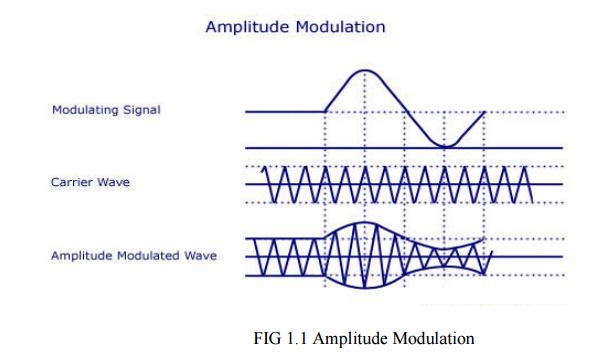
As shown above, the carrier wave has positive and negative half cycles. Both these cycles are varied according to the information to be sent. The carrier then consists of sine waves whose amplitudes follow the amplitude variations of the modulating wave. The carrier is kept in an envelope formed by the modulating wave. From the figure, you can also see that the amplitude variation of the high frequency carrier is at the signal frequency and the frequency of the carrier wave is the same as the frequency of the resulting wave.

^ü   Analysis of Amplitude Modulation Carrier Wave:

Let v_c = V_c Sin w_ct

v_m = V_m Sin w_mt

v_c – Instantaneous value of the carrier

V_c – Peak value of the carrier

W_c – Angular velocity of the carrier

v_m – Instantaneous value of the modulating signal

V_m – Maximum value of the modulating signal

w_m – Angular velocity of the modulating signal

f_m – Modulating signal frequency

It must be noted that the phase angle remains constant in this process. Thus it can be ignored.

The amplitude of the carrier wave varies at f_m.The amplitude modulated wave is given by the equation A = V_c + v_m = V_c + V_m Sin w_mt

= V_c [1+ (V_m/V_c Sin w_mt)]

= V_c (1 + mSin w_mt)

m – Modulation Index. The ratio of V_m/V_c.

Instantaneous value of amplitude modulated wave is given by the equation v = A Sin w_ct = Vc (1 + m Sin w_mt) Sin wct

= V_c Sin w_ct + mVc (Sin w_mt Sin w_ct)

v = V_c Sin wct + [mV_c/2 Cos (wc-wm)t – mVc/2 Cos (wc + wm)t]

The above equation represents the sum of three sine waves. One with amplitude of Vc and a frequency of w_c/2 , the second one with an amplitude of mV_c/2 and frequency of (w_c – w_m)/2 and the third one with an amplitude of mV_c/2 and a frequency of (w_c + w_m)/2 .

In practice the angular velocity of the carrier is known to be greater than the angular velocity of the modulating signal (w_c >> w_m). Thus, the second and third cosine equations are more close to the carrier frequency. The equation is represented graphically as shown below.

^ü Frequency Spectrum of AM Wave:

Lower side frequency – (w_c – w_m)/2

Upper side frequency – (w_c +w_m)/2

The frequency components present in the AM wave are represented by vertical lines approximately located along the frequency axis. The height of each vertical line is drawn in proportion to its amplitude. Since the angular velocity of the carrier is greater than the angular velocity of the modulating signal, the amplitude of side band frequencies can never exceed half of the carrier amplitude.

Thus there will not be any change in the original frequency, but the side band frequencies (w_c – w_m)/2 and (w_c +w_m)/2 will be changed. The former is called the upper side band (USB) frequency and the later is known as lower side band (LSB) frequency.

Since the signal frequency w_m/2 is present in the side bands, it is clear that the carrier voltage component does not transmit any information.

Two side banded frequencies will be produced when a carrier is amplitude modulated by a single frequency. That is, an AM wave has a band width from (w_c – w_m)/2 to (w_c +w_m)/2 , that is, 2w_m/2 or twice the signal frequency is produced. When a modulating signal has more than one frequency, two side band frequencies are produced by every frequency. Similarly for two frequencies of the modulating signal 2 LSB‘s and 2 USB‘s frequencies will be produced.

The side bands of frequencies present above the carrier frequency will be same as the ones present below. The side band frequencies present above the carrier frequency is known to be the upper side band and all those below the carrier frequency belong to the lower side band. The USB frequencies represent the some of the individual modulating frequencies and the LSB frequencies represent the difference between the modulating frequency and the carrier frequency. The total bandwidth is represented in terms of the higher modulating frequency and is equal to twice this frequency.

^ü   Modulation Index (m):

The ratio between the amplitude change of carrier wave to the amplitude of the normal carrier wave is called modulation index. It is represented by the letter ‗m‘.

It can also be defined as the range in which the amplitude of the carrier wave is varied by the modulating signal. m = V_m/V_c.

Percentage modulation, %m = m*100 = V_m/V_c * 100

The percentage modulation lies between 0 and 80%.

Another way of expressing the modulation index is in terms of the maximum and minimum values of the amplitude of the modulated carrier wave. This is shown in the figure below.

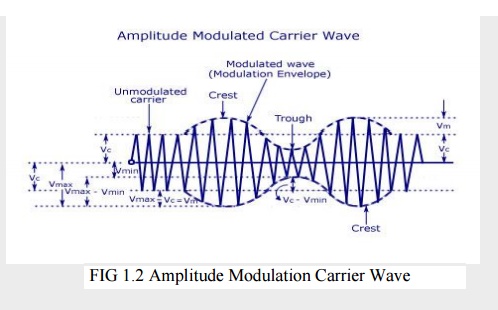
2 Vin = Vmax – Vmin

V_in = (V_max – V_min)/2

Vc = Vmax – Vin

= V_max – (V_max-V_min)/2 =(V_max + V_min)/2

Substituting the values of Vm and Vc in the equation m = Vm/Vc , we get

M = Vmax – Vmin/Vmax + Vmin

As told earlier, the value of ‗m‘ lies between 0 and 0.8. The value of m determines the strength and the quality of the transmitted signal. In an AM wave, the signal is contained in the variations of the carrier amplitude. The audio signal transmitted will be weak if the carrier wave is only modulated to a very small degree. But if the value of m exceeds unity, the transmitter output produces erroneous distortion.

^ü   Power Relations in an AM wave:

A modulated wave has more power than had by the carrier wave before modulating. The total power components in amplitude modulation can be written as:

Ptotal = Pcarrier + PLSB + PUSB

Considering additional resistance like antenna resistance R.

P_carrier = [(V_c/√2)/R]² = V²_C/2R

Each side band has a value of m/2 V_c and r.m.s value of mV_c/2√2. Hence power in LSB and USB can be written as

P_LSB = P_USB = (mV_c/2√2)²/R = m²/4*V²C/2R = m₂/4 P_carrier

P_total = V²_C/2R + [m²/4*V²C/2R] + [m²/4*V²C/2R] = V²_C/2R (1 + m²/2) = P_carrier (1 + m²/2)

In some applications, the carrier is simultaneously modulated by several sinusoidal modulating signals. In such a case, the total modulation index is given as

Mt = √(m1² + m2² + m3² + m4² + …..

If Ic and It are the r.m.s values of unmodulated current and total modulated current and R is the resistance through which these current flow, then

P_total/P_carrier = (It.R/Ic.R)² = (It/Ic)²

P_total/P_carrier = (1 + m²/2)

It/Ic = 1 + m²/2

^ü   Limitations of Amplitude Modulation:

1.     Low Efficiency- Since the useful power that lies in the small bands is quite small, so the efficiency of AM system is low.

2.     Limited Operating Range – The range of operation is small due to low efficiency. Thus, transmission of signals is difficult.

3.     Noise in Reception – As the radio receiver finds it difficult to distinguish between the amplitude variations that represent noise and those with the signals, heavy noise is prone to occur in its reception.

4.     Poor Audio Quality – To obtain high fidelity reception, all audio frequencies till 15 KiloHertz must be reproduced and this necessitates the bandwidth of 10 KiloHertz to minimise the interference from the adjacent broadcasting stations. Therefore in AM broadcasting stations audio quality is known to be poor.