Chapter: Electrical and electronics : Circuit Theory : Network Reduction and Network Theorems for DC And AC Circuits
Thevenins Theorem
THEVENINS THEOREM:
In circuit theory, Th├®venin's theorem for linear electrical networks states that any combination of voltage sources, current sources, and resistors with two terminals is electrically equivalent to a single voltage source V and a single series resistor R. For single frequency AC systems the theorem can also be applied to general impedances, not just resistors.
The procedure adopted when using Th├®veni determine the current in any branch of an active network (i.e. one containing a source of e.m.f.):
(i) remove the resistance R from that branch,
(ii) determine the open-circuit voltage, E, across the break,
remove each source of e.m.f. and replace them by their internal resistances and then determine the resistance, r, ŌĆślooking-inŌĆÖbreak.
(iv) determine the value of the current from the equivalent circuit shown in Figure 13.33, i.e. I = ER+r
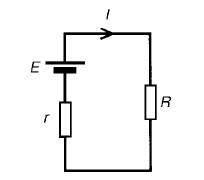
Problem 1: Use Th├®veninŌĆÖs theorem to find the current flowing in the 10 ╬® resistor for the circuit shown in Figure
Following the above procedure:
The 10 ╬®resistance is removed from the circuit as shown in Figure There is no current flowing in the 5 ╬®resistor and current I1 is given by:
I1 = 10/R1 + R2
= 10/2 + 8
= 1A
P.d. across R2 =I1R2 =1├Ś8=8V Hence p.d. across AB, i.e. the open-circuit voltage across the break, E =8V
(iii) Removing the source of e.m.f. gives the circuit of Figure Resistance, r = R3 + R1R2/R1 + R2
=5+ (2├Ś8/2+8)
= 5 + 1.6 = 6.6 ╬®
(iv) The equivalent Th├®veninŌĆÖs circuit is shown in F
Current I = E/R+r= 8/10+6.6= 8/16.6=0.482A
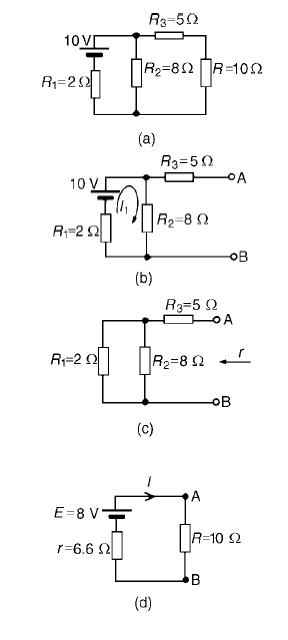
Problem 2: For the network shown in Figure determine the current in the 0.8 ╬® resistor using
Th├®veninŌĆÖs theorem.
Following the procedure:
The 0.8_ resistor is removed from the circuit as shown in Figure
Current I1 = 12/1+5+4= 12/10
=1.2A
P.d. across 4 ╬®resistor=4I1 =(4) (1.2)=4.8V
Hence p.d. across AB, i.e. the open-circuit voltage across AB, E =4.8V
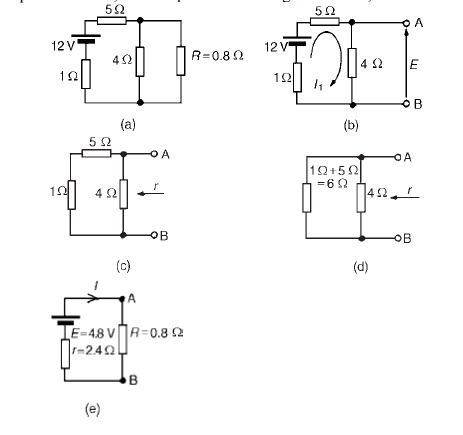
(iii) Removing the source of e.m.f. gives the circuit shown in Figure (c). The equivalent circuit of Figure
(c) is shown in Figure (d), from which,resistance r = 4├Ś6/4+6= 24/10
=2.4 ╬®
(iv) The equivalent Th├®veninŌĆÖs circuit I=E/+R is show
= 4.8/2.4+0.8
= 4.8/3.2
I = 1.5A=current in the 0.8 ╬®resistor
Problem 3: U Use Th├®veninŌĆÖs theorem to determine the current I flowing in the 4 ╬® resistor shown in Figure.
Find also the power dissipated in the 4 ╬®resistor.
(i) The 4 ╬®resistor is removed from the circuit as shown in Figure
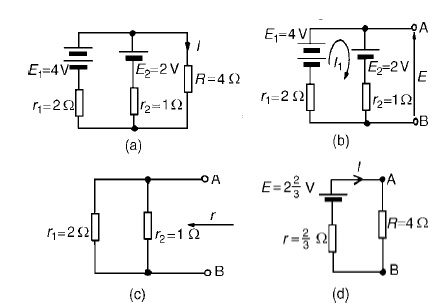
(ii) Current I1 = E1 ŌłÆE2/r1 +r2
= 4ŌłÆ2/2+1
= 2/3A
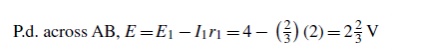
(iii) Removing the sources of e.m.f. gives the circuit shown in Figure (c), from which resistance
r = 2 ├Ś 1/2 + 1 = 2/3 ╬®
(iv)The equivalent Th├®veninŌĆÖs circuit is show
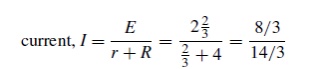
= 8/14
= 0.571A
= current in the 4 ╬®resistor
Problem 4: Power dissipated in 4 ╬®resistor,P=I2R=(0.571)2 (4)=1.304W Use Th├®veninŌĆÖs t to determine the current flowing in the 3 ╬® resistance of the network shown in Figure (a). The
voltage source has negligible internal resistance.
i) The 3 ╬®resistance is removed from the circuit as shown in Figure (b).
(ii) The 1 2/3 ╬®resistance now carries no current. P.d. across 10 ╬®resistor=(10/10+5)(24)
=16V
Hence p.d. across AB, E =16V
(iii) Removing the source of e.m.f. and replacing it by its internal resistance means that the 20 ╬®resistance is short-circuited as shown in Figure (c) since its internal resistance is zero. The 20 ╬®resistance may thus be removed as shown in Figure (d)

From Figure (d), resistance,
r =1 2/3+ 10├Ś5/10+5 =5 ╬®
(iv) The equivalent Th├®veninŌĆÖs circuit is show current, I = E/r +R= 16/3+5= 16/8
=2A
Problem 5: AWheatstone Bridge network is shown in Figure (a). Calculate the current flowing in the 32 ╬®resistor, and its direction, using Th├®veni negligible resistance.
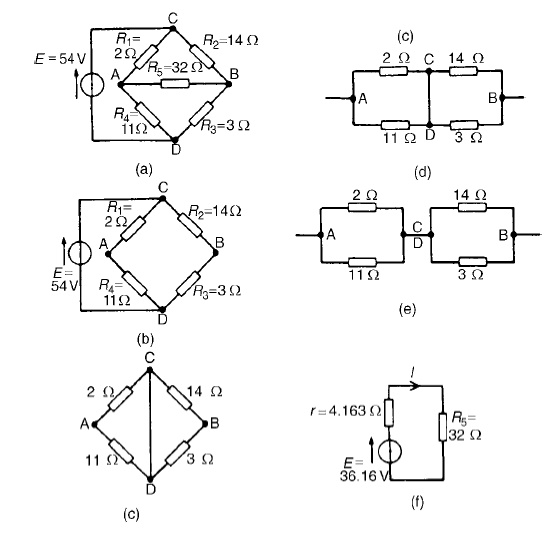
The 32 ╬®resistor is removed from the circuit as shown in Figure (b) The p.d. between A and C,
VAC =R1/R1 +R4 (E) =2/2+11(54) = 8.31V The p.d. between B and C,
VBC =R2/R2 +R3 (E) =14/14+3(54) = 44.47V Hence the p.d. between A and B=44.47ŌłÆ8.31=36.16V
Point C is at a potential of +54V. Between C and A is a voltage drop of 8.31V. Hence the voltage at point A is 54ŌłÆ8.31=45.69V. Between C and B is a voltage drop of 44.47V. Hence the voltage at point B is 54ŌłÆ44.47=9.53V. Since the voltage at A is greater than at B, current must flow in the direction A to B.
Replacing the source of e.m.f. with a short-circuit (i.e. zero internal resistance) gives the circuit shown in Figure (c). The circuit is redrawn and simplified as shown in Figure (d) and (e), from which the resistance between terminals A and B,
r = 2 ├Ś 11/2 + 11+ 14 ├Ś 3/14 + 3
= 22/13+ 42/17
= 1.692 + 2.471 = 4.163 ╬®
(iv) The equivalent Th├®veninŌĆÖs circuit is show
current I = E/r +R5
= 36.16/4.163+32 =1A
Related Topics