Spur Gears and Parallel Axis Helical Gears

SPUR GEARS AND PARALLEL AXIS HELICAL GEARS

Gear Terminology

The following terms, which will be mostly used in this chapter, should be clearly understood at this stage.

1. Pitch circle. It is an imaginary circle which by pure rolling action, would give the same motion as the actual gear

2. Pitch circle diameter. It is the diameter of the pitch circle. The size of the gear is usually specified by the pitch circle diameter. It is also called as pitch diameter.

3. Pitch point. It is a common point of contact between two pitch circles.

4. Pitch surface. It is the surface of the rolling discs which the meshing gears have replaced at the pitch circle.

5. Pressure angle or angle of obliquity. It is the angle between the common normal to two

gear teeth at the point of contact and the common tangent at the pitch point. It is usually denoted by φ. The standard pressure angles are 1 14 /2° and 20°.

6. Addendum. It is the radial distance of a tooth from the pitch circle to the top of the tooth.

7.  Dedendum. It is the radial distance of a tooth from the pitch circle to the bottom of the tooth.

8. Addendum circle. It is the circle drawn through the top of the teeth and is concentric with the pitch circle.

9. Dedendum circle. It is the circle drawn through the bottom of the teeth. It is also called

root circle.

Note : Root circle diameter = Pitch circle diameter × cos φ, where φ is the pressure angle.

10. Circular pitch. It is the distance measured on the circumference of the pitch circle from a point of one tooth to the corresponding point on the next tooth. It is usually denoted by pc. Mathematically,

Circular pitch, pc = π D/T

Where,        D = Diameter of the pitch circle, and

T = Number of teeth on the wheel.

A little consideration will show that the two gears will mesh together correctly, if the

two wheels have the same circular pitch.

Note : If D1 and D2 are the diameters of the two meshing gears having the teeth T1 and T2 respectively; then for them to mesh correctly,

11.Diametral pitch. It is the ratio of number of teeth to the pitch circle diameter in millimetres. It denoted by pd. Mathematically,

Diametral pitch,

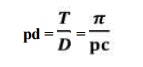
where                                                      T = Number of teeth, and

                                                                D = Pitch circle diameter.

12. Module. It is the ratio of the pitch circle diameter in millimetres to the number of teeth. It is usually denoted by m. Mathematically,

Module, m = D / T

Note : The recommended series of modules in Indian Standard are 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40 and 50.

The modules 1.125, 1.375, 1.75, 2.25, 2.75, 3.5, 4.5,5.5, 7, 9, 11, 14, 18, 22, 28, 36 and 45 are of second choice.

13.                                                                                                                                                   Clearance. It is the radial distance from the top of the tooth to the bottom of the tooth, in a meshing gear. A circle passing through the top of the meshing gear is known as clearance circle.

14.                                                                                                                                                   Total depth. It is the radial distance between the addendum and the dedendum circle of a gear. It is equal to the sum of the addendum and dedendum.

15.Working depth. It is radial distance from the addendum circle to the clearance circle. It is equal to the sum of the addendum of the two meshing gears.

16.                                                                                                                                                   Tooth thickness. It is the width of the tooth measured along the pitch circle.

17.Tooth space. It is the width of space between the two adjacent teeth measured along the pitch circle.

18.  Backlash. It is the difference between the tooth space and the tooth thickness, as measured on the pitch circle.

19.                                                                                                                                                   Face of the tooth. It is surface of the tooth above the pitch surface.

20.                                                                                                                                                   Top land. It is the surface of the top of the tooth.

21.                                                                                                                                                   Flank of the tooth. It is the surface of the tooth below the pitch surface.

22.Face width. It is the width of the gear tooth measured parallel to its axis.

23.                                                                                                                                                   Profile. It is the curve formed by the face and flank of the tooth.

24.                                                                                                                                                   Fillet radius. It is the radius that connects the root circle to the profile of the tooth.

25. Path of contact. It is the path traced by the point of contact of two teeth from the beginning to the end of engagement.

26. Length of the path of contact. It is the length of the common normal cut-off by the addendum circles of the wheel and pinion.

27.Arc of contact. It is the path traced by a point on the pitch circle from the beginning to the end of engagement of a given pair of teeth. The arc of contact consists of two parts, i.e.

(a) Arc of approach. It is the portion of the path of contact from the beginning of the engagement

to the pitch point.

(b) Arc of recess. It is the portion of the path of contact from the pitch point to the end of the engagement of a pair of teeth.

Note: The ratio of the length of arc of contact to the circular pitch is known as contact ratio i.e. number of pairs of teeth in contact.

Speed ratios and number of teeth

It is the ratio of speed of driving gear to the speed of the driven gear.

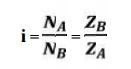
where, N_A and N_B = speed of the driver and driven respectively, and Z_A and Z_B = Number of teeth on driver and driven respectively.

Force analysis

1. Tangential component:

The tangential component F_t is a useful component. Because it transmit power. Using the value of F_t , the magnitude of torque and transmitted power can be determined.

Transmitted power W_t = F_t

2. Radial component:

The radial component F_r is a separating force which is always directed towards the centre of the gear. F_r does not really a useful component. It is also called as transverse force or bending force.

Let    P  = Power transmitted (W)

M_t = Torque transmitted (N-m)

N₁ and N₂  = Speed of pinion and gear respectively

d₁ and d₂                                                 = Pitch circle diameters of pinion and gear respectively

ϕ  = Pressure angle.

The torque transmitted by gear

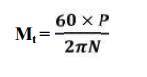
DESIGN PROCEDURE FOR SPUR GEAR:

1.                  Calculation of gear ratio (i):

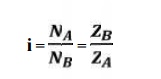
where, N_A and N_B = speed of the driver and driven respectively, and Z_A and Z_B = Number of teeth on driver and driven respectively.

2.  Selection of material

Consulting Table 5.3, knowing the gear ratio i, choose the suitable material.

3.     If not given, assume gear life (say 20000 hrs)

4.     Calculation of initial design torque:

[M_t] = M_{t .} K. K_d

where,        [M_t] = transmission torque

K   = Load factor, Table 5.11

K_d  = Dynamic load factor, Table 5.12

Assume K. K_d = 1.3 ( if not given)

5.     Calculation of E_eq, [ϭ_b] and [ϭ_c]:

ü From table 5.20 Calculate E_eq

ü From table 5.16 Calculate Design bending stress  [ϭ_b]

ü Calculate Design contact stress  [ϭ_c] by

[ϭ_c] = C_B . HB. K_cl  (or)

[ϭ_c] = C_R . HRC. K_cl

where,       C_B C_R = Coefficient of surface hardness from table 5.18

HB HRC = Hardness number

6.  Calculation if centre distance (a):

6.     Select number of teeth on gear and pinion:

Ø On pinion,Z₁ = Assume 18

Ø On gear,    Z₂ = i X Z₁

8.                                                        Calculation of module:

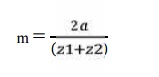
Choose standard module from table 5.8

9. Revision of centre distance(m)

10.                                                          Calculate b, d1, v and ѱp :

                                                            Calculate face width,         b = ѱ. a

                                                            Calculate pitch dia,  d        = m.z1

                                                            Calculate pitch line velocity,       v        = (πd1N1)/60

                                                            Calculate value of    ѱp  = b/d1

11. Selection of quality of gear:

Knowing the pitch line velocity and consulting table 5.22, select a suitable quality

of gear.

12. Revision of design torque [M_t]: Revise K:

Using the calculated value of ѱ_p revise the K value by using table 5.11

Revise K_d:

Using the selected quality if gear and pitch line velocity, revise the K_d

value

[M_t] = M_{t .} K. K_d

13. Check for bending:

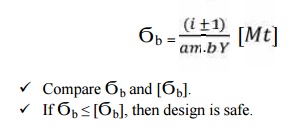
14. Check for wear strength:

Calculate induced contact stress,

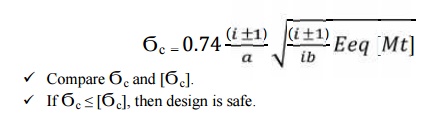
15. If the design is not satisfactory (ϭ_b > [ϭ_b] and / or ϭ_c > [ϭ_c] ), then increase the module of face width value of the gear material.

16. Check for gear:

a.      Check for bending:

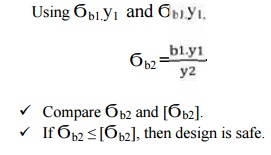
If Ϭ_b2 ≤ [Ϭ_b2], then design is safe.

b. Check for wear strength:

Calculate induced contact stress will be same for pinion and gear,

So,

Ϭ_c2 = Ϭ_c

ü Compare Ϭ_c and [Ϭ_c]

ü If Ϭ_c ≤ [Ϭ_c], then design is safe

DESIGN PROCEDURE FOR HELICAL GEAR:

1. Calculation of gear ratio (i):

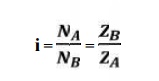
where, N_A and N_B = speed of the driver and driven respectively, and Z_A and Z_B = Number of teeth on driver and driven respectively.

2.  Selection of material

Consulting Table 5.3, knowing the gear ratio i, choose the suitable material.

3.     If not given, assume gear life (say 20000 hrs)

4.     Calculation of initial design torque:

[M_t] = M_{t .} K. K_d

where,        [M_t] = transmission torque

K   = Load factor, Table 5.11

K_d  = Dynamic load factor, Table 5.12

Assume K. K_d = 1.3 ( if not given)

5.     Calculation of E_eq, [ϭ_b] and [ϭ_c]:

ü From table 5.20 Calculate E_eq

ü From table 5.16 Calculate Design bending stress  [ϭ_b]

ü Calculate Design contact stress  [ϭ_c] by

[ϭ_c] = C_B . HB. K_cl  (or)

[ϭ_c] = C_R . HRC. K_cl

C_B C_R = Coefficient of surface hardness from table 5.18

HB HRC = Hardness number

6.  Calculation if centre distance (a):

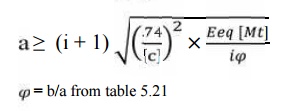
7.Select number of teeth on gear and pinion:

Ø On pinion,Z₁ = Assume ≥ 17

Ø On gear,    Z₂ = i X Z₁

8. Calculation of module:

Choose standard module from table 5.8

9. Revision of centre distance (m):

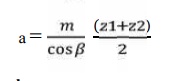
10.  Calculate b, d1, v and ѱp :      

                                                        Calculate face width,                   b = ѱ. a

                                                        Calculate pitch dia,            d        = (m_n.z₁)/ cos β

                                                        Calculate pitch line velocity,       v        = (πd₁N₁)/60

                                                        Calculate value of              ѱp  = b/d₁

11. Selection of quality of gear:

Knowing the pitch line velocity and acosulting table 5.22, select a suitable quality

of gear.

12. Revision of design torque [M_t]: Revise K:

Using the calculated value of ѱ_p revise the K value by using table 5.11

Revise K_d:

Using the selected quality if gear and pitch line velocity, revise the K_d

value

[M_t] = M_{t .} K. K_d

13. Check for bending:

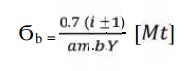
 Compare Ϭ_b and [Ϭ_b].

If Ϭ_b ≤ [Ϭ_b], then design is safe.

14. Check for wear strength:

Calculate induced contact stress,

If Ϭ_c ≤ [Ϭ_c], then design is safe.

15. If  the design is not satisfactory (ϭb > [ϭb] and / or ϭc > [ϭc] ), then increase the module of face width  value of the gear material.

16. Check for gear:

ü Compare Ϭ_b2 and [Ϭ_b2].

ü If Ϭ_b2 ≤ [Ϭ_b2], then design is safe.

d.                                                        Check for wear strength:

Calculate induced contact stress will be same for pinion and gear,

So,

Ϭc2 = Ϭc

ü Compare Ϭ_c and [Ϭ_c]

ü If Ϭ_c ≤ [Ϭ_c], then design is safe

SOLVED PROBLEMS

1.     The following particulars of a single reduction spur gear are given : Gear ratio = 10 : 1; Distance between centres = 660 mm approximately; Pinion transmits 500 kW at 1800 r.p.m.; Involute teeth of standard proportions (addendum = m) with pressure angle of 22.5°; Permissible normal pressure between teeth = 175 N per mm of width. Find :

1.  The nearest standard module if no interference is to occur;

2.  The number of teeth on each wheel;

3.  The necessary width of the pinion; and

4.     The load on the bearings of the wheels due to power transmitted.

Solution : Given :

G = TG / TP = DG / DP = 10 ;

L = 660 mm ;

P = 500 kW = 500 × 103 W;

NP = 1800 r.p.m. ; φ = 22.5° ;

WN = 175 N/mm width

1. Nearest standard module if no interference is to occur

Let    m = Required module,

TP = Number of teeth on the pinion,

TG = Number of teeth on the gear,

DP = Pitch circle diameter of the pinion, and

DG = Pitch circle diameter of the gear.

We know that minimum number of teeth on the pinion in order to avoid interference,

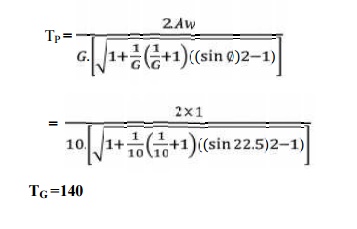
we already know that,

L = (D_G / 2) + (D_p / 2) = 5.5 D_p

We also know that

∴                                                         DP = m . TP

                                                           = DP / TP = 120 / 14

                                                           m = 8.6 mm

                                                           Since the nearest standard value of the module is 8 mm, therefore we shall take

m = 8 mm Ans.

2. Number of teeth on each wheel

We know that number of teeth on the pinion,

TP = DP / m = 120 / 8 = 15 Ans.

and number of teeth on the gear,

TG = G × TP = 10 × 15 =    150 Ans.

3. Necessary width of the pinion

We know that the torque acting on the pinion,

T = 60P/(2πN)

= 2652 N-m

Tangential load, WT = T/(D_P/2)

= 2652 / (20.12 / 2)

T  = 44200 N

WN = W_t/cosϕ

= 44200 / cos 22.5

W = 47 840 N

Since the normal pressure between teeth is 175 N per mm of width, therefore necessary width of

the pinion,

b = 47840 / 175

=273.4 mm Ans.

4. Load on the bearings of the wheels

We know that the radial load on the bearings due to the power transmitted,

WR = WN . sin φ

= 47 840 × sin 22.5°

= 18 308 N

= 18.308 kN An

2.     A bronze spur pinion rotating at 600 r.p.m. drives a cast iron spur gear at a transmission ratio of 4 : 1. The allowable static stresses for the bronze pinion and cast iron gear are 84 MPa and 105 MPa respectively. The pinion has 16 standard 20° full depth involute teeth of module 8 mm. The face width of both the gears is 90 mm. Find the power that can be transmitted from the standpoint of strength.

Solution.

Given :

NP = 600 r.p.m. ;

V.R. = TG / TP = 4 ;

σOP = 84 MPa = 84 N / mm2 ; σOG = 105 MPa = 105 N/mm2 ;

TP = 16 ;

m = 8 mm ;

b = 90 mm

We know that pitch circle diameter of the pinion,

DP = m.TP = 8 × 16 = 128 mm = 0.128 m

                                                     velocity, ∴ Pitch line         

                                                     v = πDN/60

                                                     = 4.02 m/s

 We know that for 20° full depth involute teeth, tooth form factor for the pinion,

yP = 0.154 – (.912/ T_p)

= 0.097

and tooth form factor for the gear

yG = 0.154 – (.912/ T_G)

= 0.14

σOP × yP = 84 × 0.097 = 8.148

and             σOG × yG = 105 × 0.14 = 14.7

Since (σOP × yP) is less than ( σOG × yG), therefore the pinion is weaker. Now using the Lewis equation for the pinion, we have tangential load on the tooth (or beam strength of the tooth),

WT = σwP.b.π m.yP

= (σOP × Cv) b. π m.yP (Q σWP = σOP.Cv)

= 84 × 0.427 × 90 ×  π × 8 × 0.097 = 7870 N

∴ Power that can be transmitted = WT × v

= 7870 × 4.02

= 31 640 W

= 31.64 kW Ans.

3.     A pair of helical gears are to transmit 15 kW. The teeth are 20° stub in diametral plane and have a helix angle of 45°. The pinion runs at 10 000 r.p.m. and has 80 mm pitch diameter. The gear has 320 mm pitch diameter. If the gears are made of cast steel having allowable static strength of 100 MPa; determine a suitable module and face

width from static strength considerations and check the gears for wear, given σes = 618 MPa.

Solution.

Given :

P = 15 kW = 15 × 103 W;

φ = 20° ; α = 45° ;

NP = 10 000 r.p.m. ;

DP = 80 mm = 0.08 m ;

DG = 320 mm = 0.32 m ;

σOP = σOG = 100 MPa = 100 N/mm2 ; σes = 618 MPa = 618 N/mm2

Module and face width

Let m = Module in mm, and b = Face width in mm.

Since both the pinion and gear are made of the same material (i.e. cast steel), therefore the pinion is weaker. Thus the design will be based upon the pinion.

We know that the torque transmitted by the pinion,

T = (60P) / (2πN)

= 14.32 N-m.

Tangential tooth load on the pinion,

W_T  = T / (Dp/2)

We know that number of teeth on the pinion,

TP = DP / m = 80 / m

and formative or equivalent number of teeth for the pinion, T_E = T_P / cos³ α

= 226.4 / m

∴ peripheral velocity,

v = (π Dp Np) / 60

= 42 m/s

Velocity factor,   Cv  =  0.104

Since the maximum face width (b) for helical gears may be taken as 12.5 m to 20 m, where m is the module, therefore let us take

b = 12.5 m

We know that the tangential tooth load (WT),

358 = (σOP . Cv) b.π m.y'P

= (100 × 0.104) 12.5 m ×  π m (0.175 – 0.0037 m)

= 409 m2 (0.175 – 0.0037 m)

= 72 m2 – 1.5 m3

Solving this expression by hit and trial method, we find that m = 2.3 say 2.5 mm Ans.

and face width,                            b = 12.5 m = 12.5 × 2.5 = 31.25 say 32 mm Ans.

Checking the gears for wear

We know that velocity ratio,

V.R. = D_G / D_P

=   320 / 80

= 4

We know that the maximum or limiting load for wear,

Ww = (D bQK) / cos²a

= 5554 N

A helical cast steel gear with 30° helix angle has to transmit 35 kW at 1500 r.p.m. If the gear has 24 teeth, determine the necessary module, pitch diameter and face width for 20° full depth teeth. The static stress for cast steel may be taken as 56 MPa. The width of face may be taken as 3 times the normal pitch. What would be the end thrust on the gear? The tooth factor for 20° full depth involute gear may be taken as 0.154 – 0.912/T where TE represents the equivalent number of teeth.

Solution.

Given :

α = 30° ;

P = 35 kW = 35 × 103 W ;

N = 1500 r.p.m. ;

TG = 24 ;

φ = 20° ;

σo = 56 MPa = 56 N/mm2 ; b = 3 × Normal pitch = 3 pN

Module

Let m = Module in mm, and

DG = Pitch circle diameter of the gear in mm. We know that torque transmitted by the gear,

T = (60P) / (2πN)

= 223x10³ N-mm.

Formative or equivalent number of teeth,

T_E = T_P / cos³ α

=   37.

∴ Tooth factor, y' = 0.154 – 0.912/T

= 0.129

Tangential tooth load on the pinion,

W_T  = T / (Dp/2)

_∴ = 18600 / m peripheral velocity,

v = (π Dp Np) / 60

= 1.885m m/s

Velocity factor,                                       Cv  = 0.75 / (0.75 +  v )

=  0.75 / (0.75 +  1.885m )

We know that tangential tooth load,

WT = (σo × Cv) b. π m.y' = (σo × Cv) 3pN ×  π m × y'

= (σo × Cv) 3 × pc cos  α × π m × y'

α)

= (σo × Cv) 3 π m cos α × π m × y'

...  (Q b = 3 pN)

...  (Q pN = pc cos

...  (Q pc = π m)

Solving this equation by hit and trial method, we find that

m = 5.5 say 6 mm Ans

Pitch diameter of the gear

We know that the pitch diameter of the gear,

DG = m × TG = 6 × 24 = 144 mm Ans.

Face width

It is given that the face width,

b = 3 pN = 3 pc cos α = 3 × π m cos α

= 3 × π × 6 cos 30°

= 48.98 say 50 mm Ans.

End thrust on the gear

We know that end thrust or axial load on the gear,

WA = Wr tan a

= 1790 N