Spring Deflection and Wahl's factor

SPRING DEFLECTION

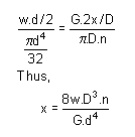
Spring striffness: The stiffness is defined as the load per unit deflection therefore

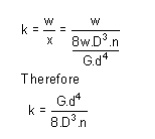
Shear stress

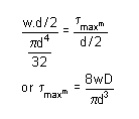
WAHL'S FACTOR :

In order to take into account the effect of direct shear and change in coil curvature a stress factor is defined, which is known as Wahl's factor.

K = Wahl' s factor and is defined as

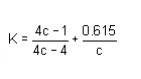
Where C = spring index

= D/d

if we take into account the Wahl's factor than the formula for the shear stress becomes

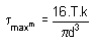
Strain Energy : The strain energy is defined as the energy which is stored within a material when the work has been done on the material.

In the case of a spring the strain energy would be due to bending and the strain energy due to bending is given by the expansion

Deflection of helical coil springs under axial loads

Deflection of springs

Example: A close coiled helical spring is to carry a load of 5000N with a deflection of 50 mm and a maximum shearing stress of 400 N/mm2 .if the number of active turns or active coils is 8.Estimate the following:

(i) wire diameter

(ii) mean coil diameter

(iii) weight of the spring.

Assume G = 83,000 N/mm2 ;   = 7700 kg/m3

solution :

(i)                for wire diametre if W is the axial load, then

Therefore,

D = .0314 x (13.317)3mm =74.15mm

D = 74.15 mm

Weight

Design of helical coil springs

Helical spring design

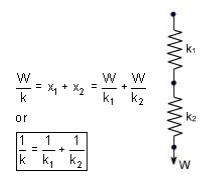
Springs in Series: If two springs of different stiffness are joined endon and carry a common load W, they are said to be connected in series and the combined stiffness and deflection are given by the following equation.

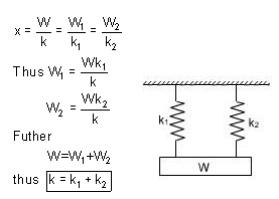
Springs in parallel: If the two spring are joined in such a way that they have a common deflection ‘x' ; then they are said t shared between the two springs and total load W = W1 + W2

stresses in helical coil springs under torsion loads

Stresses under torsion

Shear Stress in the Shaft

When a shaft is subjected to a torque or twisting, a shearing stress is produced in the shaft. The shear stress varies from zero in the axis to a maximum at the outside surface of the shaft.

The shear stress in a solid circular shaft in a given position can be expressed as:

s = T r / Ip      (1)

where

s = shear stress (MPa, psi)

T = twisting moment (Nmm, in lb)

r = distance from center to stressed surface in the given position (mm, in)

Ip = "polar moment of inertia" of cross section (mm4, in4)

The "polar moment of inertia" is a measure of an object's ability to resist torsion.

Circular Shaft and Maximum Moment

Maximum moment in a circular shaft can be expressed as:

Tmax = smax Ip / R     (2)

Where

Tmax = maximum twisting moment (Nmm, in lb)

smax = maximum shear stress (MPa, psi)

R = radius of shaft (mm, in)

Combining (2) and (3) for a solid shaft

Tmax = (p/16) smax D3    (2b)

Combining (2) and (3b) for a hollow shaft

Tmax = (p/16) smax (D4 - d4) / D        (2c)

Circular Shaft and Polar Moment of Inertia

Polar moment of inertia of a circular solid shaft can be expressed as

Ip = p R4/2 = p D4/32                (3)

D = shaft outside diameter (mm, in)

Polar moment of inertia of a circular hollow shaft can be expressed as

Ip = p (D4 - d4) /32           (3b)

where

d = shaft inside diameter          (mm, in)

Diameter of a Solid Shaft

Diameter of a solid shaft can calculated by the formula

D = 1.72 (Tmax/smax)1/3      (4)

Torsional Deflection of Shaft

The angular deflection of a torsion shaft can be expressed as

? = L T / Ip G           (5)

where

? = angular shaft deflection  (radians) L = length of shaft (mm, in)

G =  modulus of rigidity (Mpa, psi)

The angular deflection of a torsion solid shaft can be expressed as

? = 32 L T / (G p D4)     (5a)

The angular deflection of a torsion hollow shaft can be expressed as

? = 32 L T / (G p (D4- d4))       (5b)

The  angle in degrees can be achieved by multiplying the angle ? in radians with 180/p Solid shaft (p replaced)

?degrees ˜584  L T / (G D4) (6a)

Hollow shaft (p replaced)       

?degrees ˜584  L T / (G (D4- d4)   (6b)