Chapter: Civil : Mechanics Of Fluids : Fluid Kinematics And Dynamics
Solved Problems: Civil - Fluid Kinematics And Dynamics
Problem
1
A U-Tube manometer is used to measure
the pressure of water in a pipe line, which is in excess of atmospheric
pressure. The right limb of the manometer contains water and mercury is in the
left limb. Determine the pressure of water in the main line, if the difference
in level of mercury in the limbs U. U tube is 10 cm and the free surface of
mercury is in level with over the centre of the pipe. If the pressure of water
in pipe line is reduced to 9810 N/m2, Calculate the new difference
in the level of mercury. Sketch the arrangement in both cases.
Given,
Difference
of mercury = 10 cm = 0.1 m.
Let
PA = pr of water in pipe line (ie, at point A)
The point B and C lie on the same horizontal line.
Hence pressure at B should be equal to pressure at C.
But
pressure at B = Pressure at A and Pressure due to 10 cm (or) 0.1m of water.
=PA +p
´g ´h
where
, P = 1000kg/m3 and h = 0.1 m
=PA
+1000 ´9.81´0.1
=PA +981N
/ m 2


Problem
2:
A differential manometer is connected at
the two points A and B of two pipes a shown in figure. The pipe A contains a
liquid of sp. Gr = 1.5 while pipe b contains a liquid of sp . gr = 0.9 . The pressures at A and B are 1 kgf / cm2
respectively. Find the difference
in mercury level in the
differential manometer.

Problem
3
A vertical sluice gate is used to cover
an opening in a dam. The opening is 2m wide and 1.2m high. On the upstream of
the gate, the liquid of sp. Gr
1.45, lies upto a height of 1.5m above
the top of the gate, whereas on the downstream side the water is available upto
a height touching the top of the gate. Find the resultant force acting on the
gate and position of centre of pressure. Find also the force acting horizontally
at the top of the gate and posiotn of centre of pressure. Find also the force
acting horizontally at the
top
of the gate which is capable of opening it. Assume the gate is hinged at the
bottom.


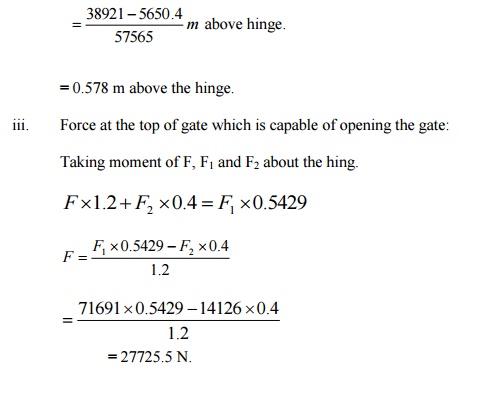
Problem 4
Find the density of a metallic body
which floats at the interface of mercury of sp. Gr 13.6 and water such that 40%
of its volume is sub-merged in
mercury
and 60% in water.

5. A
solid cylinder of diameter 4.0 m has a height of 3m. Find the meta - centric
height of the cylinder when it is floating in water with its axis vertical. The
sp gr of the cylinder -0.6 .



Problem
6
A wooden cylinder of sp. Gr = 0.6 and
circular in cross -section is required to float in oil (sp.gr = 0.90) . Find the
L/D ratio for the cylinder to float with its longitudinal axis vertical in oil,
where L is the height of cylinder and D is
its
diameters.
Solution:
Dia
of cylinder = D
Height
of cylinder = L
Sp
gr of cylinder, S1 = 0.6
Sp
gr of oil, S2 = 0.9
Let,
depth of cylinder immersed in oil = h
Buoyancy
principle
Weight
of cylinder = Weight of oil dispersed.
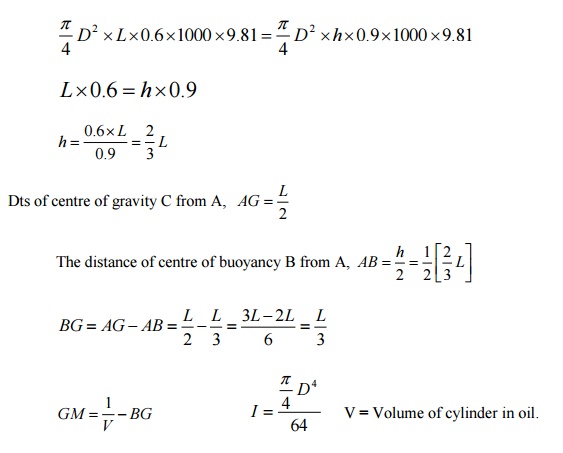

Problem
7
In a
two -two dimensional
incompressible flow, the fluid
velocity
components
are given by u = x -4y and v= - y -4x.
show that velocity potential exists and
determine its form. Find also the stream function.


1.A pipe
through which water is flowing is having diameters 20 cm and 10 cm at the
cross-sections 1 and 2 respectively. The velocity of water at section 1 is
given 4 m/s. Find the velocity head at sections 1 and 2 and also rate of
discharge.

2.The
water is flowing through a pipe having diameter 20 cm and 10 cm at sections 1
and 2 respectively. The rate of flow through pipe is 35 litres/s. The section 1
is 6 m above datum and section 2 is 4 m above datum. If the pressure at section
1 is 39.24 N/cm2, find the intensity of pressure at section 2.

3.Water
is flowing through a pipe having diameter 300 mm and 200 mm at the bottom and
upper end respectively. The intensity of pressure at the bottom end is 24.525
N/cm2 and the pressure at the upper end is 9.81 N/cm2.
Determine the difference in datum head if the rate of flow through pipe is 40
lit/s.

4.In a
two dimensional incompressible flow the fluid velocity components are given by
u = x - 4y and v = -y -
4x, Where u and v are x and y components of flow velocity. Show that the flow
satisfies the continuity equation and obtain the expression for stream
function. If the flow is potential, obtain also the expression for the velocity
potential.

5.The
stream function and velocity potential for a flow are given by ?
= 2xy and ? = x2 -
y2. Show that the
conditions for continuity and irrotational flow are satisfied. Solution:

From the
properties of Stream function, the existence
of stream function shows the possible
case of flow and if
it satisfies Laplace equation, then the
flow is irrotational.
5. A 250
mm diameter pipe carries oil of specific gravity 0.9 at a velocity of 3 m/s. At
another section the diameter is 200 mm. Find the velocity at this section and
the mass rate of flow of oil.

9.A 30 cm
x 15 cm venturimeter is inserted in a vertical pipe carring water, flowing in a
upward direction. A differential mercury manometer connected to the inlet and
throat gives a reading of 20 cm. Find the discharge. Take Cd = 0.98.

Related Topics