Solitons

SOLITONS

Group velocity dispersion (GVD) causes most pulses to broaden in time as they propagate through an fiber.

A ‘solitons’ are pulses that travel along the fiber without change in shape or amplitude or velocity.

Soliton, takes advantage of non-linear effects in silica, particularly self phase modulation (SPM) resulting from the Kerr non-linearity, to overcome the pulse-broadening effects if GVD.

The term “soliton” refers to special kinds of waves that can propagate undistorted over long distances and remain unaffected after collision with each other.

In an optical communication system, solitons are very narrow, high intensity optical pulses that retain their shape through the interaction of balancing pulse dispersion with the non-linear properties of an optical fiber.

In an relative effects of SPM and GVD are controlled just right, and the appropriate pulse shape is chosen, the pulse compression routing from SPM can exactly offset the pulse broadening effect of GVD.

Fundamental Solitons- The family of pulse that do not change in shape are called fundamental solitons.

1. SOLITONS PULSE

When a pulse transverse a medium with a positive GVD parameter β2 for the constituent frequencies, the leading part of the pulse is shifted toward a longer wavelength (lower frequencies) so that the speed in that portion increases.

In the trailing half, the frequency arises. So the speed decreases. This causes the trailing edge to be further delayed.

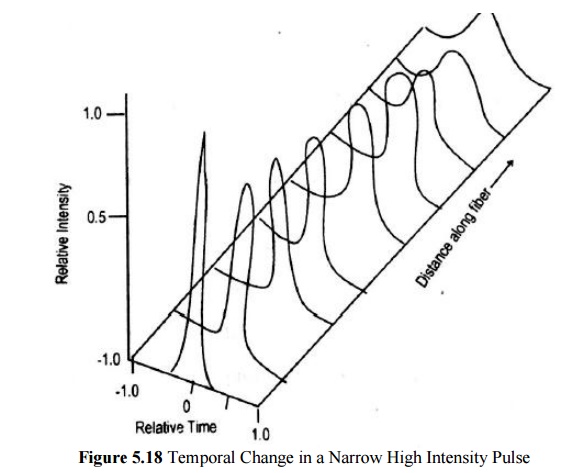
When a narrow high-intensity pulse traverse a medium with a negative GVD parameter for the constituting frequencies, GVD counteracts the chirp produced by SPM.

GND retards the low frequencies in the front end of the pulse and advances the high frequencies at the back.

The result is that the high-intensity sharply peaked soliton pulse changes neither its shape nor its spectrum as it travels along the fiber.

To derive the evolution of the pulse shape required for sodium transmission, one needs to consider the non-linear schrodinger (NLS) equation

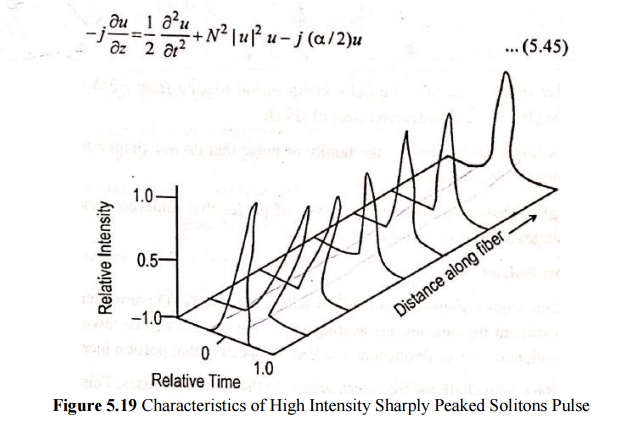
Special soliton units to eliminate scaling constants.

The Three Right-Hand Terms in Equation (5.45)

(1)  The first term represents GVD effects of the fiber.

(2)  The second non-linear term denotes the fact that the refractive index of the fiber depends on the light intensity.

Through the self-modulation process, this physical phenomenon broadens the frequency spectrum of a pulse.

(3)  The third term represents the effects of energy loss or gain.

2. SOLITONS PARAMETERS

Full-Width Half-Maximum (FWHM)

The full-width Half-maximum (FWHM) is a pulse is defined as the full width of the pulse at its half-maximum power level.

The FWHM Ts of the fundamental soliton pulse in normalized time is found from the relationship

Dispersion Length (Ldisp)

The normalized distance parameter (also called dispersion length) Ldisp is a characteristic length for the effects of the dispersion term.

Ldisp is a measure of the period of a soliton

The solition to equation (5.45) for the fundamental solution is given by

Where sech (t) is the hyperbolic secant function. This is a bell-shaped pulse.

The phase term exp (jz/2) in equation (5.46) has no influence on the shape of the pulse, the soliton is independent of z and hence is non-dispersive in the time domain.

For the NLS equation, to find the first-order effects of the dispersive and non-linear terms are just complementary phase shifts.

For a given by equation (5.46), these phase shifts are

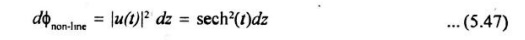
For the non-linear process, and

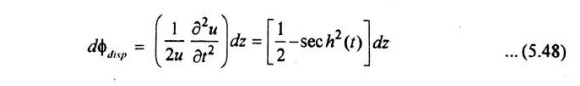
Dispersion and non-linear phase shifts of a soliton pulse which sum is constant, which yields a common phase shift of z\2 for the entire pulse.

Since such a phase shift changes neither the temporal nor the spectral shape of a pulse, the soliton remains completely non-dispersive in both the temporal and frequency domain.