Shear force and Bending Moment in beams

Shear force and Bending Moment in beams

Concept of Shear Force and Bending moment in beams:

When the beam is loaded in some arbitrarily manner, the internal forces and moments are developed and the terms shear force and bending moments come into pictures which are helpful to analyze the beams further. Let us define these terms

Now let us consider the beam as shown in fig 1(a) which is supporting the loads P1, P2, P3 and is simply supported at two points creating the reactions R1 and R2respectively. Now let us assume that the beam is to divided into or imagined to be cut into two portions at a section AA. Now let us assume that the resultant of loads and reactions to the left of AA is

„F' vertically upwards, and equilibrium,since thusthe resultant of forces to the right of A a shear force. The shearing force at any x-section of a beam represents the tendency for the portion of the beam to one side of the section to slide or shear laterally relative to the other portion.

Therefore,                            now   we   are   in   a   position   t

At any x-section of a beam, the shear for components of the forces acting on either side of the x-section.

Sign Convention for Shear Force:

The usual sign conventions to be followed for the shear forces have been illustrated in figures 2 and 3.

Bending Moment:

Let us again consider the beam which is simply supported at the two prints, carrying loads P1, P2 and P3 and having the reactions R1 and R2 at the supports Fig 4. Now, let us imagine that the beam is cut into two potions at the x-section AA. In a similar manner, as done for the case of shear force, if we say that the resultant moment about the section AA of all the loads and reactions to the left of the x-section at AA is M in C.W direction, then moment of forces to the right of x-section AA must be „M' in C. moment and is abbreviated as B.M. Now one can define the bending moment to be simply as the algebraic sum of the moments about an x-section of all the forces acting on either side of the section

Sign Conventions for the Bending Moment:

For the bending moment, following sign conventions may be adopted as indicated in Fig 5

and Fig 6.

Some times, the terms „Sagging' and negative bending moments respectively.

Bending Moment and Shear Force Diagrams:

The diagrams which illustrate the variations in B.M and S.F values along the length of the beam for any fixed loading conditions would be helpful to analyze the beam further.

Thus, a shear force diagram is a graphical plot, which depicts how the internal shear force „F' varieslength ofalongbeam.Ifx dentotesthethe length of the beam, then F is function x i.e. F(x).

Similarly a bending moment diagram is a graphical plot which depicts how the internal bending moment „M' varies along theM(x)l.

Basic Relationship Between The Rate of Loading, Shear Force and Bending Moment:

The construction of the shear force diagram and bending moment diagrams is greatly simplified if the relationship among load, shear force and bending moment is established.

Let us consider a simply supported beam AB carrying a uniformly distributed load w/length.

Let us imagine to cut a short slice o from the origin „0'.

Let us detach this portion of the beam and draw its free body diagram.

The forces acting on the free body diagram of the detached portion of this loaded beam are the following

•             The   shearingdFat theforcesectionxandFx + andxrespectivelyF+.

•              The   bending   momentdx beatMandtheM+dMsectionsrespectively.

• Force due to external loading, if „ total loading on this slice of length dx is w. dx, which is approximately acting through the centre „c'. If theobeuniformlyloadingdistributed thenisit wouldassumedpassexactly through the centre „c'.

This small element must be in equilibrium under the action of these forces and couples.

Now              let   us   take   the   moments   at   the   po

Conclusions: From the above relations,the following important conclusions may be drawn

•             From Equation (1), the area of the basic calculus is the bending moment diagram

•             The   slope   of   bending   moment   diagram

Thus, if F=0; the slope of the bending moment diagram is zero and the bending moment is therefore constant.'

•             The   maximum   or   minimum   Bending   mome

The slope of the shear force diagram is equal to the magnitude of the intensity of the distributed loading at any position along the beam. The –ve sign is as a consequence of our particular choice of sign conventions

Procedure for drawing shear force and bending moment diagram:

Preamble:

The advantage of plotting a variation of shear force F and bending moment M in a beam as a function of „x' measured from one end maximum absolute value of shear force and bending moment.

Further, the determination of valueramount importance so as to determine the value of deflection of beam subjected to a given loading.

Construction of shear force and bending moment diagrams:

A shear force diagram can be constructed from the loading diagram of the beam. In order to draw this, first the reactions must be determined always. Then the vertical components of forces and reactions are successively summed from the left end of the beam to preserve the mathematical sign conventions adopted. The shear at a section is simply equal to the sum of all the vertical forces to the left of the section.

When the successive summation process is used, the shear force diagram should end up with the previously calculated shear (reaction at right end of the beam. No shear force acts through the beam just beyond the last vertical force or reaction. If the shear force diagram closes in this fashion, then it gives an important check on mathematical calculations.

The bending moment diagram is obtained by proceeding continuously along the length of beam from the left hand end and summing up the areas of shear force diagrams giving due regard to sign. The process of obtaining the moment diagram from the shear force diagram by summation is exactly the same as that for drawing shear force diagram from load

diagram.

It may also be observed that a constant shear force produces a uniform change in the bending moment, resulting in straight line in the moment diagram. If no shear force exists along a certain portion of a beam, then it indicates that there is no change in moment takes place. It may also further observe that dm/dx= F therefore, from the fundamental theorem of calculus the maximum or minimum moment occurs where the shear is zero. In order to check the validity of the bending moment diagram, the terminal conditions for the moment must be satisfied. If the end is free or pinned, the computed sum must be equal to zero. If the end is built in, the moment computed by the summation must be equal to the one calculated initially for the reaction. These conditions must always be satisfied.

Cantilever beams - problems

Cantilever with a point load at the free end:

M_x = - w.x

A cantilever   of   length   carries   a   conc

Draw shear force and bending moment.

Solution:

At a section a distance x from free end consider the forces to the left, then F = -W (for all values of x) -ve sign means the shear force to the left of the x-section are in downward direction and therefore negative

Taking moments about the section gives (obviously to the left of the section)

M = -Wx (-ve sign means that the moment on the left hand side of the portion is in the anticlockwise direction and is therefore taken as –ve according to the sign convention)

so that the maximum bending moment occurs at the fixed end i.e. M = -W l

Simply supported beam -problems

Simply supported beam subjected to a central load (i.e. load acting at the mid-way)

By symmetry the reactions at the two supports would be W/2 and W/2. now consider any section X-X from the left end then, the beam is under the action of following forces.

.So the shear force at any X-section would be = W/2 [Which is constant upto x < l/2]

If we consider another section Y-Y which is beyond l/2 then

for all values greater = l/2

SSB with central point load:

Overhanging beams - problems

In the problem given below, the intensity of loading varies from q1 kN/m at one end to the q2 kN/m at the other end.This problem can be treated by considering a U.d.i of intensity q1 kN/m over the entire span and a uniformly varying load of 0 to ( q2- q1)kN/m over the entire span and then super impose teh two loadings.

Point of Contraflexure:

Consider the loaded beam a shown below along with the shear force and Bending moment diagrams for It may be observed that this case, the bending moment diagram is completely positive so that the curvature of the beam varies along its length, but it is always concave upwards or sagging.However if we consider a again a loaded beam as shown below along with the S.F and B.M diagrams, then

It may be noticed that for the beam loaded as in this case,

The bending moment diagram is partly positive and partly negative.If we plot the deflected shape of the beam just below the bending moment

This diagram shows that   L.H.S   of   the   beam   „sags'

The point C on the beam where the curvature changes from sagging to hogging is a point of contraflexure.

OR

It corresponds to a point where the bending moment changes the sign, hence in order to find the point of contraflexures obviously the B.M would change its sign when it cuts the X-axis therefore to get the points of contraflexure equate the bending moment equation equal to zero.The fibre stress is zero at such sections

Note: there can be more than one point of contraflexure 2.4Stresses in beams

Preamble:

When a beam having an arbitrary cross section is subjected to a transverse loads the beam will bend. In addition to bending the other effects such as twisting and buckling may occur, and to investigate a problem that includes all the combined effects of bending, twisting and buckling could become a complicated one. Thus we are interested to investigate the bending effects alone, in order to do so, we have to put certain constraints on the geometry of the beam and the manner of loading.

Assumptions:

The constraints put on the geometry would form the assumptions:

1. Beam is initially straight , and has a constant cross-section.

2.  Beam is made of homogeneous material and the beam has a longitudinal plane of symmetry.

3. Resultant of the applied loads lies in the plane of symmetry.

4. The geometry of the overall member is such that bending not buckling is the primary cause of failure.

5. Elastic limit is nowhere exceeded and ‘E'issame in tension and compression.

6. Plane cross - sections remains plane before and after bending.

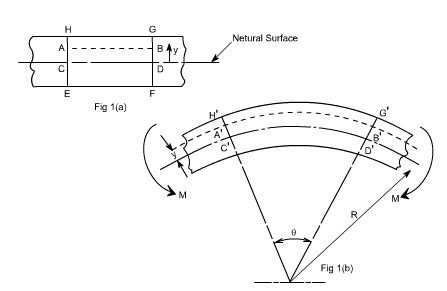
Let us consider a beam initially unstressed as shown in fig 1(a). Now the beam is subjected to a constant bending moment (i.e. „ obtained by applying equal couples at each end. The beam will bend to the radius R as shown in Fig 1(b)

As a result of this bending, the top fibers of the beam will be subjected to tension and the bottom to compression it is reasonable to suppose, therefore, that some here between the two there are points at which the stress is zero. The locus of all such points is known as neutral axis . The radius of curvature R is then measured to this axis. For symmetrical sections the N. A. is the axis of symmetry but what ever the section N. A. will always pass through the centre of the area or centroid.

As we are aware of the fact internal reactions developed on any cross-section of a beam may consists of a resultant normal force, a resultant shear force and a resultant couple. In order to ensure that the bending effects alone are investigated, we shall put a constraint on the loading such that the resultant normal and the resultant shear forces are zero on any cross-section perpendicular to the longitudinal axis of the member, That means F = 0 since or M = constant.

Thus, the zero shear force means that the bending moment is constant or the bending is same at every cross-section of the beam. Such a situation may be visualized or envisaged when the beam or some portion of the beam, as been loaded only by pure couples at its ends. It must be recalled that the couples are assumed to be loaded in the plane of symmetry.

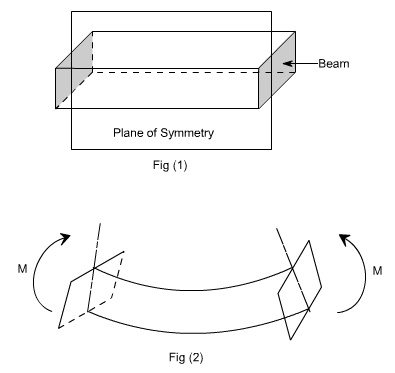
When a member is loaded in such a fashion it is said to be in pure bending. The examples of pure bending have been indicated in EX 1and EX 2 as shown below :

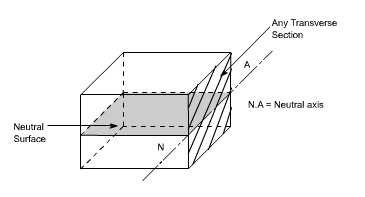
When a beam is subjected to pure bending are loaded by the couples at the ends, certain cross-section gets deformed and we shall have to make out the conclusion that,

1.Plane sections originally perpendicular to longitudinal axis of the beam remain plane and perpendicular to the longitudinal axis even after bending , i.e. the cross-section A'E', B'F' ( refer Fig 1(a) ) do not get warped or curved.

2. In the deformed section, the planes of this cross-section have a common intersection i.e. any time originally parallel to the longitudinal axis of the beam becomes an arc of circle.

We know that when a beam is under bending the fibres at the top will be lengthened while at the bottom will be shortened provided the bending moment M acts at the ends. In between these there are some fibres which remain unchanged in length that is they are not strained, that is they do not carry any stress. The plane containing such fibres is called neutral surface.

The line of intersection between the neutral surface and the transverse exploratory section is called the neutral axisNeutral axis (N A) .

Bending Stresses in Beams or Derivation of Elastic Flexural formula :

In order to compute the value of bending stresses developed in a loaded beam, let us consider the two cross-sections of a beam HE and GF , originally parallel as shown in fig 1(a).when the beam is to bend it is assumed that these sections remain parallel i.e. H'E' and G'F' , the final position of the sections, are still straight lines, they then subtend some angle q.                     

Consider now fiber AB in the material, at adistance y from the N.A, when the beam bends this will stretch to A'B' 

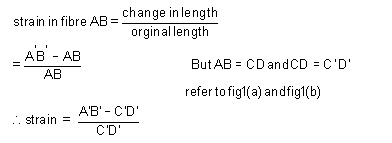
Since CD and C'D' are on the neutral axis and it is assumed that the Stress on the neutral axis zero. Therefore, there won't be any strain on the neutral axis. 

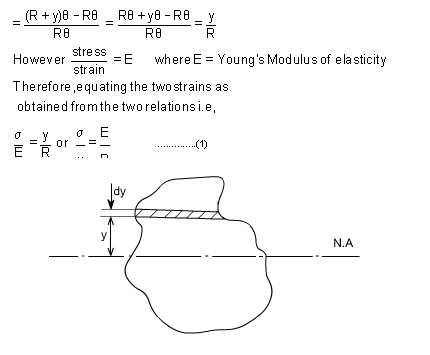
Consider any arbitrary a cross-section of beam, as shown above now the strain on a fibre at a distance   „y'   from   the   N.A,   is   given   b Now the termis the property of the material and is called as a second moment of area of the cross-section and is denoted by a symbol I.

Therefore M/I = sigma/y = E/R

This equation is known as the Bending Theory Equation.The above proof has involved the assumption of pure bending without any shear force being present. Therefore this termed as the pure bending equation. This equation gives distribution of stresses which are normal to cross-section i.e. in x-direction.        

                   Stress variation along the length and in the beam section Bending Stress and Deflection Equation

                   In this section, we consider the case of pure bending; i.e., where only bending stresses exist as  a  result  of  applied  bending  moments.  To  develop  the  theory,  we  will  take  the phenomenological approach to develop   whatEuleris-Bernoullicalledtheoryof beamth bending.”Geometry: Consider a long slender straight beam of length L and cross-sectional area A. We assume the beam is  prismatic or nearly so. The length dimension is large compared to the dimensions  of the cross-section. While the cross-section may be any shape,          we will assume that it is symmetric about the y axis Loading: For our purposes, we will consider shear forces or distributed loads that are applied in the y direction only (on the surface of the beam) and moments about the z-axis. We have consider examples of such loading in ENGR 211 previously and some examples are shown below:        

                   Kinematic Observations:   In   order   to   obtain a   “fee beam subjected to pure bending loads, it is informative to conduct an experiment. Consider a rectangular lines have   been   scribed   on   the   beam’ bottom surfaces (and thus parallel to a centroidally placed x-axis along the length of the beam).  Lines  are  also  scribed  around  the  circumference  of  the  beam  so  that  they  are perpendicular to the longitudinals (these circumferential lines form flat planes as shown).

                   The longitudinal and circumferential lines form a square grid on the surface. The beam is now bent by moments at each end as shown in the lower photograph. After loading, we note

that the top line has stretched and the bottom line has shortened (implies that there is strain exx). If measured carefully, we see that the longitudinal line at the center has not changed length (implies that exx = 0 at y = 0). The longitudinal lines now appear to form concentric circular lines.

We also note that the vertical lines originally perpendicular to the longitudinal lines remain straight

and perpendicular to the longitudinal lines. If measured carefully, we will see that the vertical lines remain approximately the same length (implies eyy = 0). Each of the vertical lines (as well as the planes they form) has rotated and, if extended downward, they will pass through a common point that forms the center of the concentric longitudinal lines (with some radius ?). The flat planes originally normal to the longitudinal axis remain essentially flat planes and remain normal to the deformed longitudinal lines. The squares on the surface are now quadrilaterals and each appears to have tension (or compression) stress in the longitudinal direction (since the horizontal lines of a square have changed length). However, in pure bending we make the assumption that. If the x-axis is along the length of beam and the y-axis is normal to the beam, this suggests that we have an axial normal stress sxx that is tension above the x-axis and compression below the y-axis. The remaining normal stresses syy and szz will generally be negligible for pure bending about the z-axis. For pure bending, all shear stresses are assumed to be zero. Consequently, for pure bending, the stress matrix reduces to zero