One Dimensional Heat Transfer Element

ONE DIMENSIONAL HEAT TRANSFER ELEMENT

In structural problem displacement at each nodel point is obtained. By using these displacement solutions, stresses and strains are calculated for each element. In structural problems, the unknowns are represented by the components of vector field. For example, in a two dimensional plate, the unknown quantity is the vector field u(x,y),where u is a (2x1)displacement vector.

Heat transfer can be defined as the transmission of energy from one region another region due to temperature difference. A knowledge of the temperature distribution within a body is important in many engineering problems. There are three modes of heat transfer.

They are:    (i) Conduction

(ii) Convection

(iii)Radiation

1Strong Form for Heat Conduction in One Dimension with Arbitrary Boundary Conditions

Following the same procedure as in Section, the portion of the boundary where the temperature is prescribed, i.e. the essential boundary is denoted by  T and the boundary where the flux is prescribed is recommended for  Science  and  Engineering  Track.  Denoted by q ;  these  are  the boundaries  with  natural  boundary  conditions. These  boundaries  are complementary, so

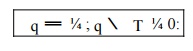
With the unit normal used in , we can express the natural boundary condition as qn ¼ q. For example, positive flux q causes heat inflow (negative q ) on the left boundary point where qn ¼ q ¼ q and heat outflow (positive q ) on the right boundary point where qn ¼ q ¼ q.

Strong form for 1D heat conduction problems

2Weak Form for Heat Conduction in One Dimension with Arbitrary Boundary Conditions

We again multiply the first two equations in the strong form by the weight function and integrate over the domains over which they hold, the domain for the differential equation and the domain q for the flux boundary condition, which

yields ws dx with w ¼

T and combining with gives

Recalling that w ¼ 0 on

Weak form for 1D heat conduction problems

Find T ðxÞ 2 U such that

Notice the similarity between