Types of annuities

Types of annuities

a) Based on the number of periods:

(i) Certain annuity: An annuity payable for a fixed number of years is called certain annuity.

Installments of payment for a plot of land, Bank security deposits, purchase of domestic durables are examples of certain annuity. Here the buyer knows the specified dates on which installments are to be made.

(ii) Annuity contingent: An annuity payable at regular interval of time till the happening of a specific event or the date of which cannot be accurately foretold is called annuity contingent.

For example the endowment funds of trust, where the interest earned is used for welfare activities only. The principal remains the same and activity continues forever.

All the above types of annuities are based on the number of their periods. An annuity can also be classified on the basis of mode of payment as under.

b) Based on the mode of payment :

(i) Ordinary annuity: An annuity in which payments of installments are made at the end of each period is called ordinary annuity (or immediate annuity)

For example repayment of housing loan, vehicle loan etc.,

ii) Annuity due: An annuity in which payments of installments are made in the beginning of each period is called annuity due.

In annuity due every payment is an investment and earns interest. Next payment will earn interest for one period less and so on, the last payment will earn interest of one period.

For example saving schemes, life insurance payments, etc.,

The derivation of the following formulae are given for better understanding and are exempted from examination

(i) Amount of immediate annuity (or) Ordinary annuity (or) Certain annuity

Let ‘a’ be the ordinary annuity and i percent be the rate of interest per period. In ordinary annuity, the first installment is paid after the end of first period. Therefore it earns interest for (n – 1) period, second installment earns interest for (n – 2) periods and so on. The last installment earns for (n – n) periods. (i.e) earns no interest.

For (n–1) periods,

The amount of first annuity    = a(1+i) ^n-1

(ii)  Present Value of immediate annuity (or ordinary annuity)

Let ‘a’ be the annual payment of an ordinary annuity, n be the number of years and i percent be the interest on one rupee per year and P be the present value of the annuity. In the case of immediate annuity, payments are made periodically at the end of specified  period. Since the first installment is paid at the end of first year, its present value is a / 1+i , the present value of second installment is a / (1+i)² and so on. If the present value of last installment is a / (1+i)ⁿ , then we have

(iii) Amount of annuity due at the end of n period

Annuity due is an annuity in which the payments are made at the beginning of each payment period. The first installment will earn interest for n periods at the rate of ‘i’ percent per period. Similarly second installment will earn interest for (n – 1) periods, and so on the last interest for on period.

(iv) Present value of annuity due

Since the first installment is paid at the beginning of the first period (year), its present value will be the same as ‘a’, the annual payment of annuity due. The second installment is paid in the beginning of the second year, hence its present value is given a / (1+ i) and so on. The last installment is paid in the beginning of nth year, hence its present value is given as a / (1+ i)^n-1

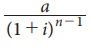
If P denotes the present value of annuity due, then

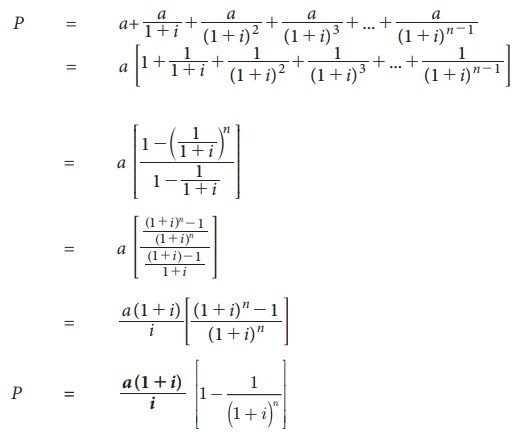
(v)     Perpetual Annuity

Perpetual annuity is an annuity whose payment continuous for ever. As such the amount of perpetuity is undefined as the amount increases without any limit as time passes on. We know that the present value P of immediate annuity is given by

Now as per the definition of perpetual annuity as n → ∞, we know that 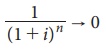 since 1+i > 1.

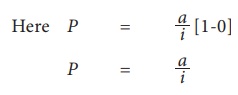
NOTE

In all the above formulae the period is of one year. Now if the payment is made more than once in a year then ‘i’ is replaced by i/k and n is replaced by nk, where k is the number of payments in a year.