Types of Diagrams

Types of Diagrams

In practice, varieties of diagrams are used to present the data. They are explained below.

Simple Bar Diagram

Simple bar diagram can be drawn either on horizontal or vertical base. But, bars on vertical base are more common. Bars are erected along the axis with uniform width and space between the bars must be equal. While constructing a simple bar diagram, the scale is determined as proportional to the highest value of the variable. The bars can be coloured to make the diagram attractive. This diagram is mostly drawn for categorical variable. It is more useful to present the data related to the fields of Business and Economics.

Example 4.1

The production cost of the company in lakhs of rupees is given below.

i. Construct a simple bar diagram.

ii. Find in which year the production cost of the company is (a) maximum (b) minimum (c) less than 40 lakhs.

iii. What is the average production cost of the company?

iv. What is the percentage increase from 2014 to 2015?

Solution:

(i) We represent the above data by simple bar diagram in the following manner:

Step-1: Years are marked along the X-axis and labelled as ‘Year’.

Step-2: Values of Production Cost are marked along the Y-axis and labelled as ‘Production Cost (in lakhs of `).

Step-3: Vertical rectangular bars are erected on the years marked and whose height is proportional to the magnitude of the respective production cost.

Step-4: Vertical bars are filled with the same colours.

The simple bar diagram is presented in Fig.4.1.

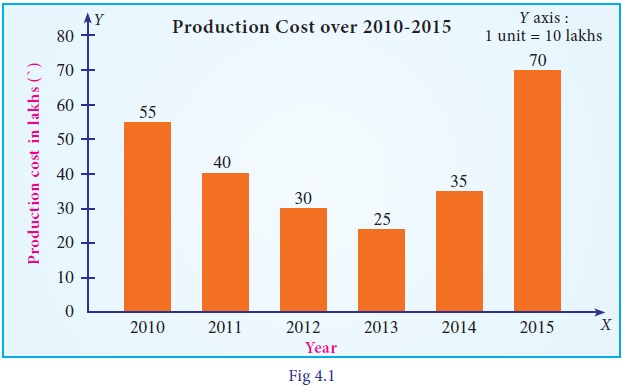
(ii) (a) The maximum production cost of the company was in the year 2015.

(b) The minimum production cost of the company was in the year 2013.

(c) The production cost of the company during the period 2012- 2014 is less than 40 lakhs.

iii. Average production Cost of the company

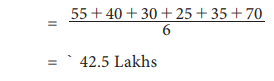
iv. Percentage increase in the production cost of the company is

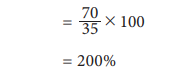
Pareto Diagram:

Vilfredo  Pareto  (1848-1923),  born  in  Paris  in  an Italian  aristocratic  family,  studied  Engineering  and Mathematics at the University of Turin. During his studies at the University of Lousane in Switzerland, Pareto derived a complicated mathematical formula to prove the distribution of income and wealth in society is not random. Approximately 80% of total wealth in a society lies with only 20% of the families. The famous law about the ‘Vital few and trivial many’ is widely known as ‘Pareto Principle’ in Economics.

Pareto diagram is similar to simple bar diagram. But, in Pareto diagram, the bars are arranged in the descending order of the heights of the bars. In addition, there will be a line representing the cumulative frequencies (in %) of the different categories of the variable. The line is more useful to find the vital categories among trivial categories.

Example 4.2

Administration of a school wished to initiate suitable preventive measures against breakage of equipment in its Chemistry laboratory. Information collected about breakage of equipment occurred during the year 2017 in the laboratory are given below:

Draw Pareto Diagram for the above data. Which equipment requires more attention in order to reduce breakages?

Solution:

Since we have to find the vital few among the several, we draw Pareto diagram.

Step 1 : Arrange the equipment according to the descending order of the number of breakages.

Step 2 : Find the percentage of breakages for each equipment using the formula No. of Breakages

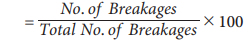
Step 3 : Calculate cumulative percentage for each equipment.

Step 4 : Mark the equipment along the X-axis and the number of breakages along the Y-axis. Construct an attached simple bar diagram to this data. In an attached simple bar diagram, the vertical bars are erected adjacently.

Step 5 : Mark the cumulative no. of breakages for each equipment corresponding to the mid-point of the respective vertical bar.

Step 6 : Draw a free hand curve joining those plotted points.

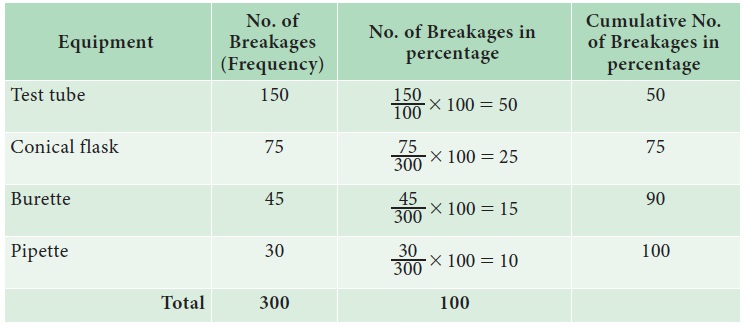
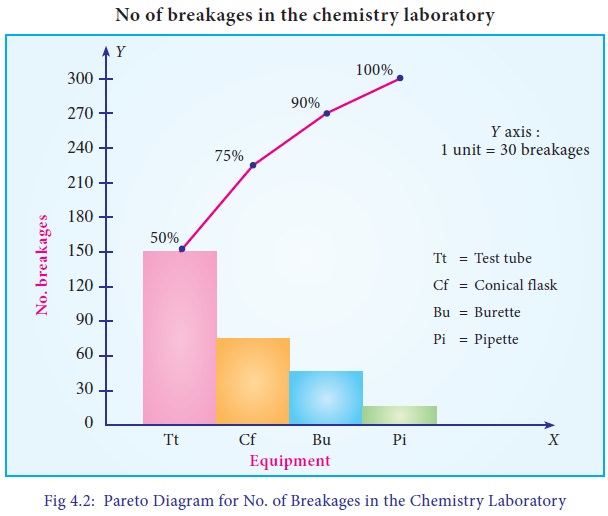
From Fig 4.2, it can be found that 50% of breakages is due to Test tube, 25% due to Conical Flask. Therefore, the School Administration has to focus more attention on reducing the breakages of Test Tubes and Conical Flasks.

Multiple Bar Diagram

Multiple bar diagram is used for comparing two or more sets of statistical data. Bars with equal width are placed adjacently for each cluster of values of the variable. There should be equal space between clusters. In order to distinguish bars in each cluster, they may be either differently coloured or shaded. Legends should be provided.

Example 4.3

The table given below shows the profit obtained before and after tax payment(in lakhs of rupees) by a business man on selling cars from the year 2014 to 2017.

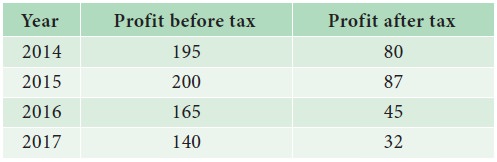
a.        Construct a multiple bar diagram for the above data.

b.        In which year, the company earned maximum profit before paying the tax?

c.         In which year, the company earned minimum profit after paying the tax?

d.        Find the difference between the average profit earned by the company before paying the tax and after paying the tax.

Solution:

Since we are comparing the profit earned before and after paying the tax by the same Company, the multiple bar diagram is drawn. The diagram is drawn following the procedure presented below:

Step 1 : Years are marked along the X-axis and labeled as “Year”.

Step 2 : Values of Profit before and after paying the tax are marked along the Y-axis and labeled as “Profit (in lakhs of `)”.

Step 3 : Vertical rectangular bars are erected on the years marked, whose heights are proportional to the respective profit. The vertical bars corresponding to the profit earned before and after paying the tax in each year are placed adjacently.

Step 4 : The vertical bars drawn corresponding to the profit earned before paying the tax are filled with one type of colour. The vertical bars drawn corresponding to the profit earned after paying the tax are filled with another type of colour. The colouring procedure should be applied to all the years uniformly.

Step 5 : Legends are displayed to describe the different colours applied to the bars drawn for profit earned before and after paying the tax.

The multiple bar diagram is presented in Fig 4.3.

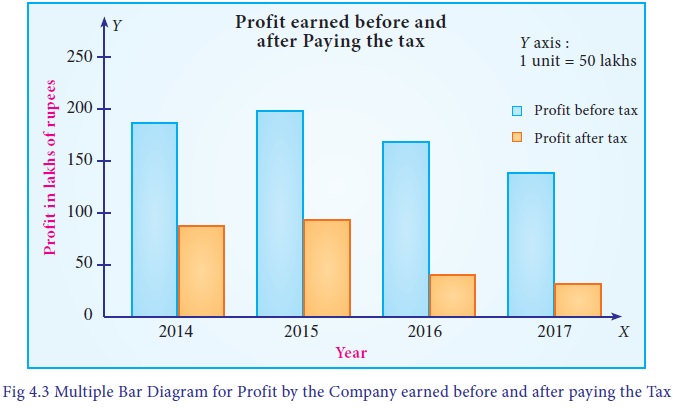
(i) The company earned the maximum profit before paying the tax in the year 2015.

(ii) The company earned the minimum profit after paying the tax in the year 2017.

(iii) The average profit earned before paying the tax = 700/4 = 175lak

 The average profit earned after paying the tax = 244/4 = 61 lakhs

Hence, difference between the average profit earned by the company before paying the tax and after paying the tax is = 175 – 61 = ` 114 lakhs.

Component Bar Diagram(Sub-divided Bar Diagram)

A component bar diagram is used for comparing two or more sets of statistical data, as like multiple bar diagram. But, unlike multiple bar diagram, the bars are stacked in component bar diagrams. In the construction of sub-divided bar diagram, bars are drawn with equal width such that the heights of the bars are proportional to the magnitude of the total frequency. The bars are positioned with equal space. Each bar is sub-divided into various parts in proportion to the values of the components. The subdivisions are distinguished by different colours or shades. If the number of clusters and the categories in the clusters are large, the multiple bar diagram is not attractive due to more number of bars. In such situation, component bar diagram is preferred.

Example 4.4

Total expenditure incurred on various heads of two schools in an year are given below. Draw a suitable bar diagram.

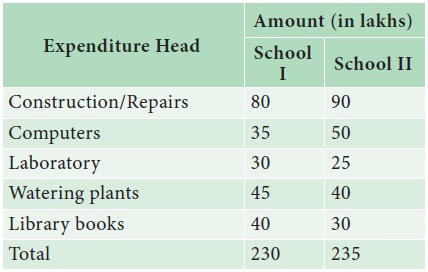
Which school had spent more amount for

(a) construction/repairs (b) Watering plants?

Solution : 

Since we are comparing the amount spent by two schools in a year towards various expenditures with respect to their total expenditures, a component bar diagram is drawn.

Step 1 : Schools are marked along the X-axis and labeled as “School”.

Step 2 : Expenditure Head are marked along the Y-axis and labeled as “Expenditure (` in lakhs)”.

Step 3 : Vertical rectangular bars are erected for each school, whose heights are proportional to their respective total expenditure.

Step 4 : Each vertical bar is split into components in the order of the list of expenditure heads. Area of each rectangular box is proportional to the frequency of the respective expenditure head/component. Rectangular boxes for each school are coloured with different colours. Same colours are applied to the similar expenditure heads for each school.

Step 5 : Legends are displayed to describe the colours applied to the rectangular boxes drawn for various expenditure heads.

The component bar diagram is presented in Fig 4.4.

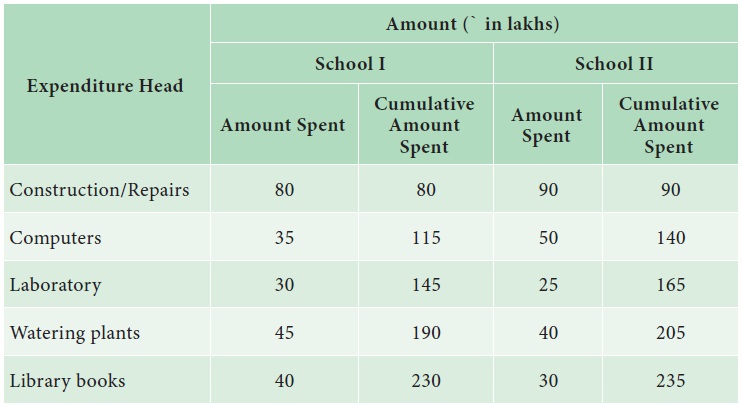
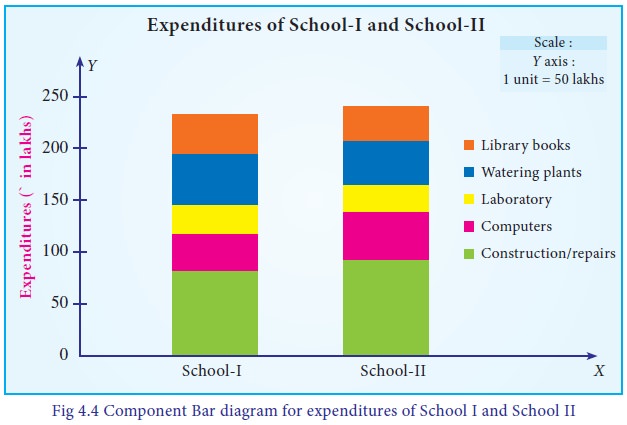
(i) School- II had spent more amount towards Construction/Repairs.

(ii) School- I had spent more amount towards Watering plants.

Percentage Bar Diagram

Percentage bar diagram is another form of component bar diagram. Here, the heights of the components do not represent the actual values, but percentages. The main difference between sub-divided bar diagram and percentage bar diagram is that, in the former, the height of the bars corresponds to the magnitude of the value. But, in the latter, it corresponds to the percentages. Thus, in the component bar diagram, heights of the bars are different, whereas in the percentage bar diagram, heights are equal corresponding to 100%. Hence, percentage bar diagram will be more appealing than sub-divided bar diagram. Also, comparison between components is much easier using percentage bar diagram.

Example 4.5

Draw the percentage sub-divided bar diagram to the data given in Example 4.4. Also find 

(i) The percentage of amount spent for computers in School I 

(ii) What are the expenditures in which School II spent more than School I. 

Solution:

Since we are comparing the amount spent by two schools in a year towards various expenditures with respect to their total expenditures in percentages, a percentage bar diagram is drawn. 

Step 1 : Schools are marked along the X-axis and labeled as “School”. 

Step 2 : Amount spent in percentages are marked along the Y-axis and labeled as “Percentage of Expenditure (` in lakhs)”. 

Step 3 : Vertical rectangular bars are erected for each school, whose heights are taken to be hundred. 

Step 4 : Each vertical bar is split into components in the order of the list of percentage expenditure heads. Area of each rectangular box is proportional to the percentage of frequency of the respective expenditure head/component. Rectangular boxes for each school are coloured with different colours.  Same colours are applied to the similar expenditure heads for each school. 

Step 5 : Legends are displayed to describe the colours applied to the rectangular boxes drawn for various expenditure heads.

The percentage bar diagram is presented in Fig 4.5.

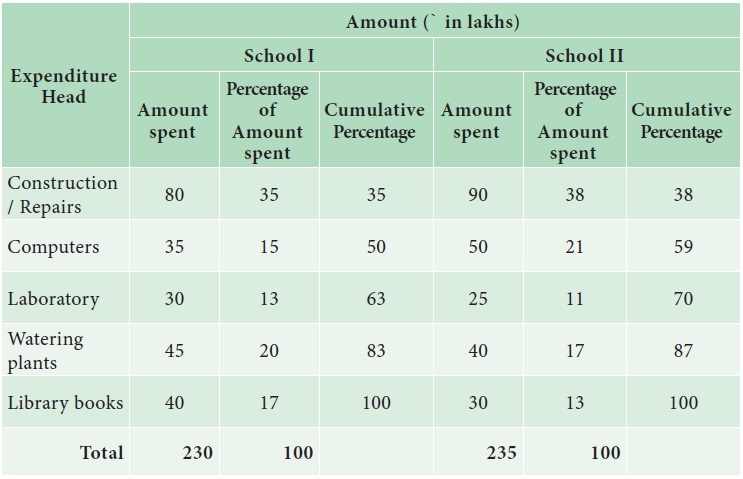
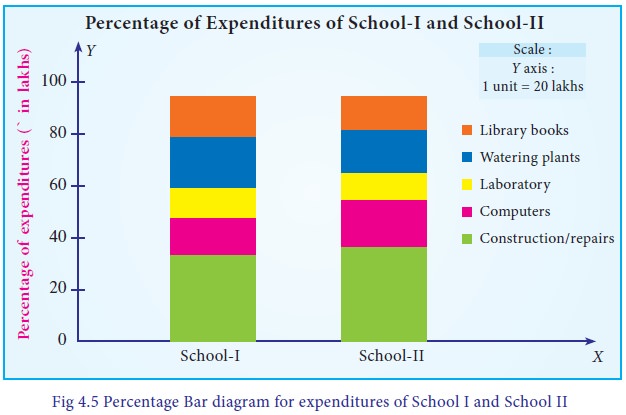
i. 21% of the amount was spent for computers in School I

ii. 38% of expenditure was spent for construction/Repairs by School II than School I.

Pie Diagram

The Pie diagram is a circular diagram. As the diagram looks like a pie, it is given this name. A circle which has 360c is divided into different sectors. Angles of the sectors, subtending at the center, are proportional to the magnitudes of the frequency of the components.

Procedure:

The following procedure can be followed to draw a Pie diagram for a given data:

i.               Calculate total frequency, say, N.

ii.               Compute angles for each component using the formula.

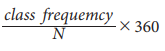
iii.               Draw a circle with radius of sufficient length as a horizontal line.

iv.               Draw the first sector in the anti-clockwise direction at an angle calculated for the first component.

v.               Draw the second sector adjacent to the first sector at an angle corresponding to the second component.

vi.               This process may be continued for all the components.

vii.               Shade/colour each sector with different shades/colours.

viii.               Write legends to each component.

Example 4.6

Draw a pie diagram for the following data (in hundreds) of house hold expenditure of a family.

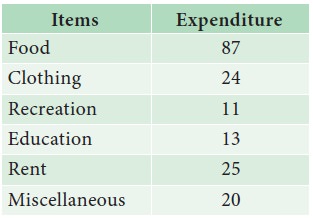
Also find

i. The central angle of the sector corresponding to the expenditure incurred on Education

ii. By how much percentage the recreation cost is less than the Rent.

Solution :

The following procedure is followed to draw a Pie diagram for a given data:

i. Calculate the total expenditure, say, N.

ii. Compute angles for each component  food, clothing, recreation, education, rent and miscellaneous using the formula class frequency/N x 360

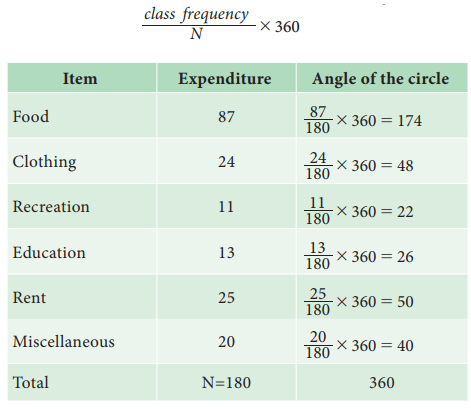
iii. Draw a circle with radius of sufficient length as a horizontal line.

iv. Draw the first sector in the anti-clockwise direction at an angle calculated for the first component food.

v. Draw the second sector adjacent to the first sector at an angle corresponding to the second component clothing.

vi. This process is continued for all the components namely recreation, education, rent and miscellaneous.

i.               Shade/colour each sector with different shades/colours.

viii. Write legends to each component.

The pie diagram is presented in Fig 4.6.

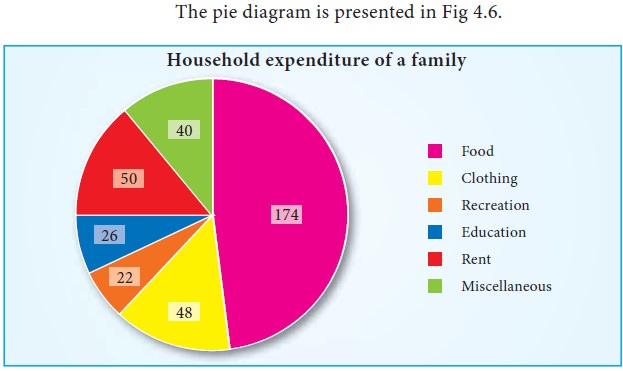
The central angle of the sector corresponding to the expenditure incurred on Education is 26^o

Recreation cost is less than rent by 28^o

Pictogram

Pictograms are diagrammatic representation of statistical data using pictures of resemblance. These are very useful in attracting attention. They are easily understood. For the purpose of propaganda, the pictorial presentations of facts are quite popular and they also find places in exhibitions. They are extensively used by the government organizations as well as by private institutions. If needed, scales can be fixed.

Despite its visual advantages, pictogram has limited application due to the usage of pictures resembling the data. It can express an approximate value than the given actual numerical value.

Example 4.7

The following table gives the sugarcane production in tonnes per acre for various years.

Represent the above data by pictogram.

Solution :

The above data is represented by pictogram in the following manner:

Example 4.8

The Pictogram given below shows the number of persons who have traveled by train from Chennai to Rameshwaram on each day of a week

From the Pictogram find: 

i. Number of travelers travelled during the week

ii. On which day there was a maximum rush in the train

iii. The difference between the maximum and minimum number of travelers. 

Solution :

i. Here total number of  is 48, and each  represents 100 persons. Hence number of travelers travelled during the week is 48×100=4800.

ii. The maximum rush in the train is on Thursday.

iii. Maximum number of persons travelled on Thursday = 10 

Hence the number of persons travelled on Thursday is 10×100 = 1000

Minimum number of persons travelled on Wednesday = 4

Hence the number of persons travelled on Wednesday is 4×100=400 

Therefore difference between maximum and minimum number of travelers is 1000-400=600 persons.