Definition, Formula, Solved Example Problems, Exercise | Mathematics - Trigonometric ratios | 11th Business Mathematics and Statistics(EMS) : Chapter 4 : Trigonometry
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 4 : Trigonometry
Trigonometric ratios
Trigonometric ratios
1. Quadrants:
Let X' OX and Y' OY be two lines at right
angles to each other as in the figure. We call X' OX and Y' OY as X axis and Y
axis respectively. Clearly these axes divided the entire plane into four equal
parts called “Quadrants” .
The parts XOY, YOX' , X'OY' and Y'OX are known
as the first, second, third and the fourth quadrant respectively.
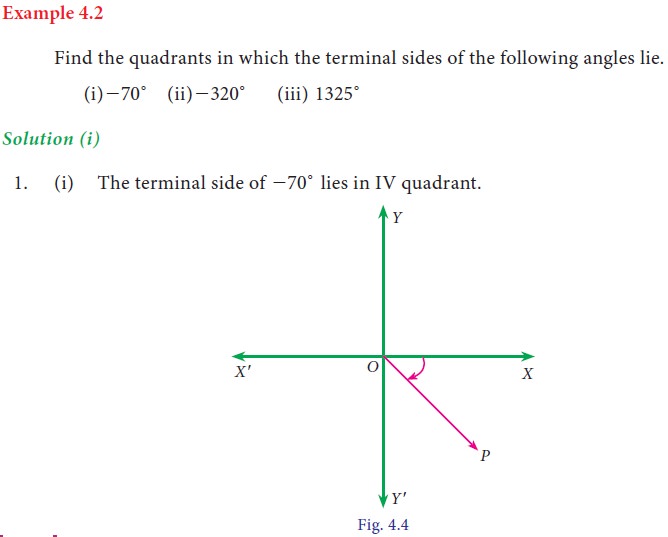
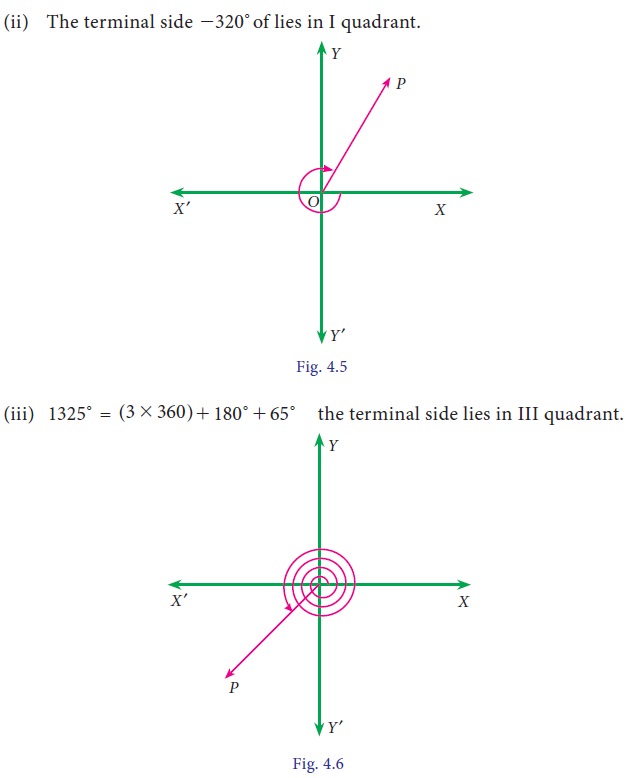
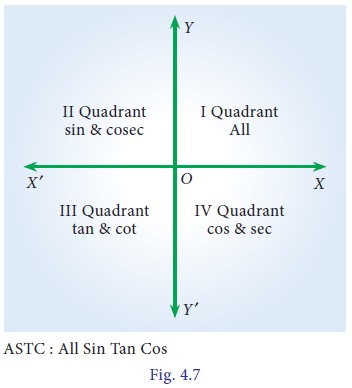
2. Signs of the trigonometric ratios of an angle θ as it varies from 0º to 360º
In the first quadrant both x and y are positive. So
all trigonometric ratios are positive. In the second quadrant (90° < θ <180°) x is
negative and y is positive. So
trigonometric ratios sin θ and cosec θ are positive. In the third quadrant (180° < θ <
270°) both x and y are negative. So trigonometric ratios
tan θ and cot θ are positive. In the fourth quadrant (270° < θ < 360° ) x is positive and y is negative. So trigonometric ratios cos θ and sec θ are positive.

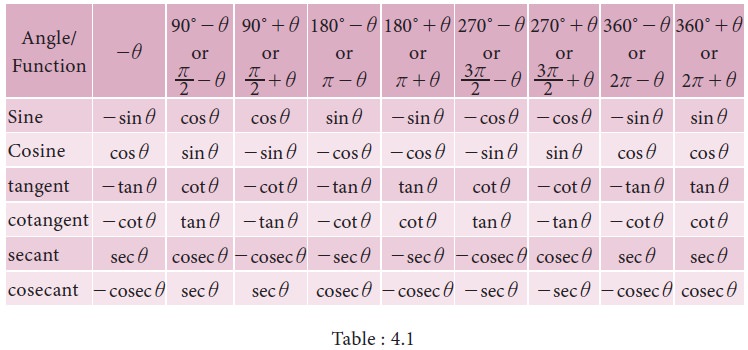
3. Trigonometric ratios of allied angles:
Two angles are said to be allied angles when
their sum or difference is either zero or a multiple of 90° . The angles -θ , 90°
± θ, 180° ± θ,, 360° ± θ etc .,are angles allied to
the angle θ. Using trigonometric ratios of the allied angles we can find the
trigonometric ratios of any angle.


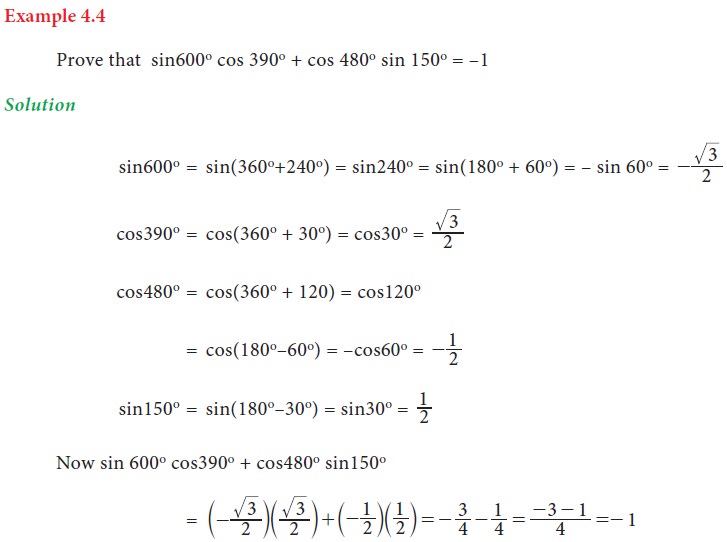
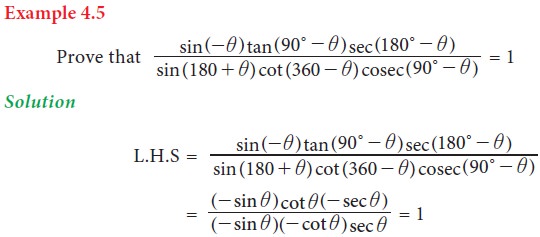


Related Topics