The Security of RSA

The Security of RSA

Four possible approaches to attacking the RSA algorithm are

•             Brute force: This involves trying all possible private keys.

•             Mathematical attacks: There are several approaches, all equivalent in effort to factoring the product of two primes.

•             Timing attacks: These depend on the running time of the decryption algorithm.

•             Chosen ciphertext attacks: This type of attack exploits properties of the RSA algorithm.

The defense against the brute-force approach is the same for RSA as for other cryptosystems, namely, to use a large key space. Thus,the larger the number of bits   in d, the better. However, because the calculations involved, both in key generation and inencryption/decryption, are complex, 

the larger the size of the key, the slower the system will run.

In this subsection, we provide an overview of mathematical and timing attacks.

THE FACTORING PROBLEM We can identify three approaches to attacking RSA mathematically.

1.                                                                   Factor n into its two prime factors. This enables calculation of ϕ(n) = (p - 1) ´

(q - 1), which in turn enables determination of d K e-1 (mod ϕ(n)).

2.                                                                   Determine ϕ(n) directly, without first determining p and q. Again, this enables determination of d K e-1 (mod ϕ(n)).

3.                                                                   Determine d directly, without first determining ϕ(n).

Most discussions of the cryptanalysis of RSA have focused on the task of fac- toring n into its two prime factors. Determining f(n)given n is equivalent to factor- ing n [RIBE96]. With presently known algorithms, determining d given e and n appears to be at least as time-consuming as the factoring problem [KALI95]. Hence, we can use factoring performance as a benchmark against which to evaluate the security of RSA.

For a large n with large prime factors, factoring is a hard problem, but it is not as hard as it used to be. A striking illustration of this is thefollowing. In 1977, the three inventors of RSA dared Scientific American readers to decode a cipher they printed in Martin Gardner’s“Mathematical Games” column [GARD77]

.

 They offered a $100 reward for the return of a plaintext sentence, an event they predictedmight not occur for some 40 quadrillion years. In April of 1994, a group working over the Internet claimed the prize after only eightmonths of work [LEUT94]. 

This challenge used a public key size (length of n) of 129 decimal digits, or around 428 bits. In the meantime,just as they had done for DES, RSA Laboratories had issued challenges for the RSA cipher with key sizes of 100, 110, 120, and so on,digits. The latest challenge to be met is the RSA-200 challenge with a key length of 200 decimal digits, or about 663 bits. Table 9.5shows the results to date. The level of effort is measured in MIPS-years: a

Table 9.5    Progress in Factorization

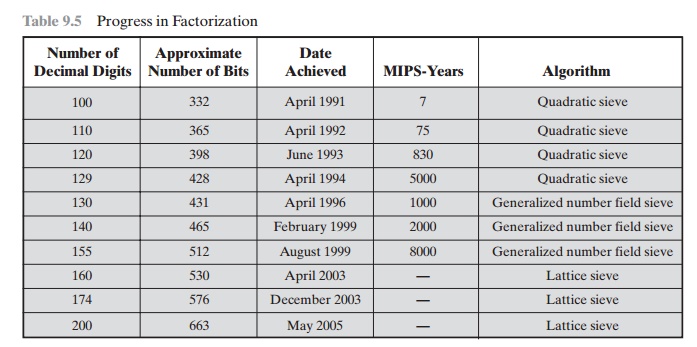
million-instructions-per-second processor running for one year, which is about 3 ´x 1013 instructions executed. A 1 GHz Pentium isabout a 250-MIPS  machine.

A striking fact about Table 9.5 concerns the method used. Until the mid-1990s, factoring attacks were made using an approach known as the quadratic sieve. The attack on RSA-130 used a newer algorithm, the generalized number field sieve (GNFS), and was able to factor a larger number than RSA-129 at only 20% of the computing effort.

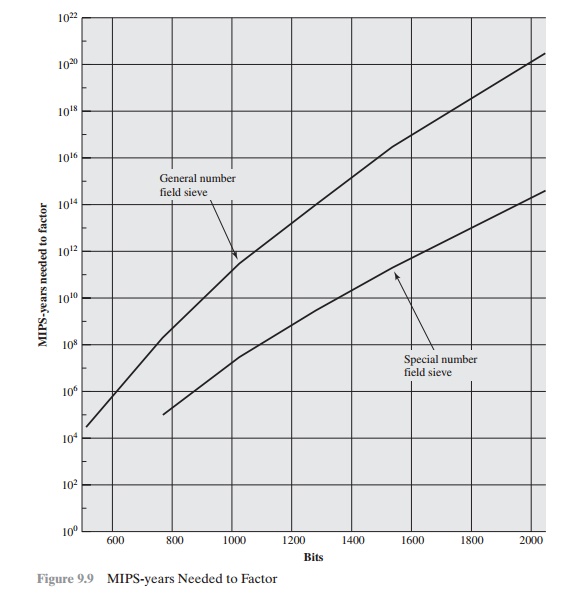
The threat to larger key sizes is twofold: the continuing increase in computing power and the continuing refinement of factoringalgorithms. We have seen that the move to a different algorithm resulted in a tremendous speedup. We can expect further refinements inthe GNFS, and the use of an even better algorithm is also a possibility. In fact, a related algorithm, the special number field sieve (SNFS),can factor numbers with a specialized form considerably faster than the generalized number field sieve. Figure 9.9 compares theperformance of the two algorithms. It is reasonable to expect a breakthrough that would enable a general factoring performance in aboutthe same time as SNFS, or even better [ODLY95]. Thus, we need to be careful in choosing a key size for RSA. For the near future, a keysize in the range of 1024 to 2048 bits seems reasonable.

In addition to specifying the size of n, a number of other constraints have been suggested by researchers. To avoid values of n that maybe factored more easily, the algorithm’s inventors suggest the following constraints on p and q.

1.    p and q should differ in length by only a few digits. Thus, for a 1024-bit key (309 decimal digits), both p and q should be on the order ofmagnitude of 1075 to 10100.

2.    Both (p - 1) and (q - 1) should contain a large prime factor.

3.    gcd( p - 1, q - 1) should be small.

In addition, it has been demonstrated that if e < n and d < n1/4, then d can be easily determined [WIEN90].

TIMING ATTACKS If one needed yet another lesson about how difficult it is to assess the security of a cryptographic algorithm, theappearance of timing attacks provides a stunning one. Paul Kocher, a cryptographic consultant, demonstrated that a snooper candetermine a private key by keeping track of how long a computer takes to decipher messages [KOCH96, KALI96b]. Timing attacks areapplicable not just to RSA, but to other public-key cryptography systems. This attack is alarming for two reasons: It comes from acompletely unexpected direction, and it is a ciphertext-only attack.

A timing attack is somewhat analogous to a burglar guessing the combination of a safe by observing how long it takes for someone toturn the dial from number to number. We can explain the attack using the modular exponentiation algorithm of Figure 9.8, but theattack can be adapted to work with any implementation that does not run in fixed time. In this algorithm, modular exponentiation isaccomplished bit by bit, with one modular multiplication performed at each iteration and an addi- tional modular multiplicationperformed for each 1 bit.

As Kocher points out in his paper, the attack is simplest to understand in an extreme case. Suppose the target system uses a modularmultiplication function that is very fast in almost all cases but in a few cases takes much more time than an entire average modular exponentiation. The attack proceeds bit-by-bit starting with   the

leftmost bit, bk. Suppose that the first j bits are known (to obtain the entire exponent, start with j = 0 and repeat the attack until the entire exponent is known). For a given ciphertext, the attacker can complete the first j iterations of the for loop. The operation of the subsequentstep depends on the unknown exponent bit. If the bit is set, d ; (d ´ a) mod n will be executed. For a few values of a and d, the modularmultiplication will be extremely slow, and the attacker knows which these are.Therefore, if the observed time to execute the decryptionalgorithm is always slow when this particular iteration is slow with a 1 bit, then this bit is assumed to be 1. If a number of observedexecution times for the entire algorithm are fast, then this bit is assumed to be 0.

In practice, modular exponentiation implementations do not have such extreme timing variations, in which the execution time of a single iteration can exceed the mean execution time of the entire algorithm. Nevertheless, there is enough variation to make this attack practical. For details, see [KOCH96].

Although the timing attack is a serious threat, there are simple countermea- sures that can be used, including the following.

•            Constant exponentiation time: Ensure that all exponentiations take the same amount of time before returning a result. This is asimple fix but does degrade performance.

•            Random delay: Better performance could be achieved by adding a random delay to the exponentiation algorithm to confuse the timing attack. Kocher points out that if defenders don’t add enough noise, attackers could still succeed by collecting additionalmeasurements to compensate for the random delays.

•            Blinding: Multiply the ciphertext by a random number before performing exponentiation. This process prevents the attackerfrom knowing what cipher- text bits are being processed inside the computer and therefore prevents the bit-by-bit analysis essentialto the timing attack.

RSA Data Security incorporates a blinding feature into some of its products.

The private-key operation M = Cd mod n is implemented as follows.

1.                  Generate a secret random number r between 0 and n - 1.

2.                  Compute C' = C(re) mod n, where e is the public exponent.

3.                  Compute M' = (C')d mod n with the ordinary RSA implementation.

4.                  Compute M = M'r-1 mod n. In this equation, r-1 is the multiplicative inverse of r mod n; see Chapter 4 for a discussion of this concept. It can be demonstrated that this is the correct result by observing that red mod n = r mod   n.

RSA Data Security reports a 2 to 10% performance penalty for blinding.

CHOSEN  CIPHERTEXT ATTACK  AND  OPTIMAL ASYMMETRIC  ENCRYPTION  PADDING The

basic RSA algorithm is vulnerable to a chosen ciphertext attack (CCA). CCA is defined as an attack in which the adversarychooses a number of ciphertexts and is then given the corresponding plaintexts, decrypted with the target’s private key. Thus, theadversary could select a plaintext, encrypt it with the target’s public key, and then be able to get the plaintext back by having itdecrypted with the private key. Clearly, this provides the adversary with no new information. Instead, the adversary exploits propertiesof RSA and selects blocks of data that, when processed using the target’s private key, yield information needed for cryptanalysis.

A simple example of a CCA against RSA takes advantage of the following property of RSA:

E(PU, M1) ´ E(PU, M2) = E(PU, [M1 ´ M2])                                     (9.2)

We can decrypt C = Me mod n using a CCA as follows.

1.                  Compute X = (C ´ 2e) mod n.

2.                  Submit X as a chosen ciphertext and receive back Y = Xd mod n. But now note that

X = (C mod n) * (2e mod n)

= (Me mod n) * (2e mod n)

= (2M)e mod n

Therefore, Y = (2M) mod n. From this, we can deduce M. To overcome this simple attack, practical RSA-based cryptosystemsrandomly pad the plaintext prior to encryption. This randomizes the ciphertext so that Equation (9.2) no longer holds. However,more sophisticated CCAs are possible, and a simple padding with a random value has been shown to be insufficient to provide the desired security. To counter such attacks, RSA Security Inc., a leading RSA vendor and former holder of the RSA patent, recommends modifying the plaintext using a procedure known as optimal asymmetric encryption padding (OAEP). A fulldiscussion of the threats and OAEP are beyond our scope; see [POIN02] for an introduction and [BELL94a] for a thorough analysis.Here, we simply summarize the OAEP procedure.

Figure 9.10 depicts OAEP encryption. As a first step, the message M to be encrypted is padded.A set of optional parameters, P, ispassed through a hash function, H.8 The output is then padded with zeros to get the desired length in the overall data

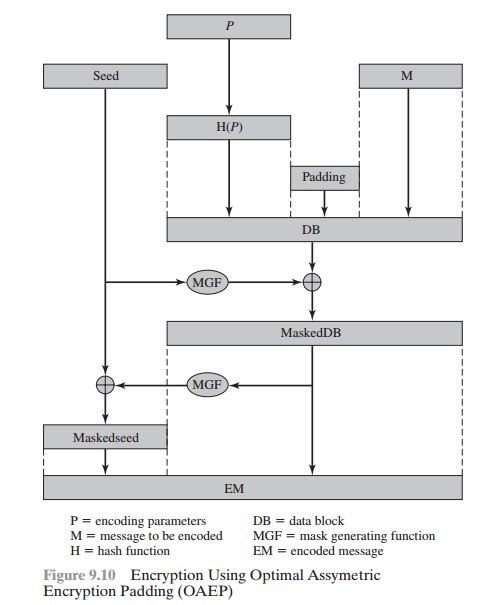
block (DB). Next, a random seed is generated and passed through another hash func- tion, called the mask generating function (MGF).The resulting hash value is bit-by-bit XORed with DB to produce a maskedDB. The maskedDB is in turn passed through the MGF toform a hash that is XORed with the seed to produce the masked seed.The concatenation of the maskedseed and the maskedDB forms theencoded message EM. Note that the EM includes the padded message, masked by the seed, and the seed, masked by the maskedDB.The EM is then encrypted using RSA.