Chapter: Cryptography and Network Security Principles and Practice : Asymmetric Ciphers : Public-Key Cryptography and RSA
Principles of Public-Key Cryptosystems and its Applications, Requirements, Cryptanalysis
PRINCIPLES
OF PUBLIC-KEY CRYPTOSYSTEMS
The concept of public-key cryptography evolved from an attempt to attack two
of the most difficult problems associated with symmetric encryption. The first
problem is that of key distribution, which is examined
in some detail
in Chapter 14.
As Chapter 14 discusses, key distribution under
symmetric encryption requires either (1) that two communicants already
share a key, which
somehow has been dis-
tributed to them; or (2) the use of a key distribution center. Whitfield Diffie,
one of the discoverers of public-key encryption (along with Martin Hellman, both at Stanford University at the time), reasoned
that this second requirement negated
the very essence of cryptography: the ability to maintain total secrecy
over your own communication. As Diffie put it [DIFF88], “what good would it do after
all to develop impenetrable
cryptosystems, if their users were forced to share their keys with a KDC that could be compromised by either burglary
or subpoena?”
The second
problem that Diffie pondered, and one that was apparently unrelated to the first,
was that of digital signatures. If the use of cryptography was to become
widespread, not just in military
situations but for commercial and private purposes,
then electronic messages and documents would need the equiv- alent of signatures used in paper documents. That is, could a method be devised that would
stipulate, to the satisfaction of all parties, that a digital message had been sent by a particular person? This
is a somewhat broader requirement than that of
authentication, and its characteristics
and ramifications are explored in
Chapter 13.
Diffie and Hellman achieved an astounding breakthrough in 1976 [DIFF76 a, b] by coming up with a method that addressed both problems and was radically different from all previous approaches to cryptography, going back over four millennia.
In the next subsection, we look at the overall
framework for public-key cryp- tography. Then we examine the requirements for the
encryption/decryption algo- rithm that is at the heart of the scheme.
Public-Key Cryptosystems
Asymmetric algorithms rely on one key for encryption
and a different but related key for decryption. These algorithms have the
following important characteristic.
•
It is
computationally infeasible to determine the decryption key given only knowledge of the cryptographic algorithm and the encryption key.
In addition, some algorithms, such as RSA, also exhibit
the following characteristic.
•
Either of the two related keys can be used for encryption, with the other used
for decryption.
•
A public-key encryption scheme has six
ingredients (Figure 9.1a; compare with Figure 2.1).
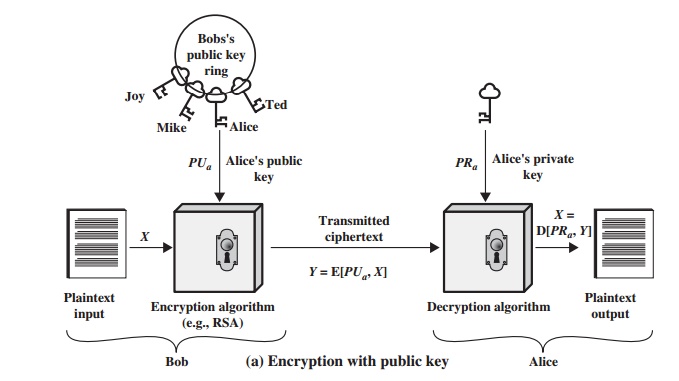
•
Plaintext: This is the readable message
or data that is fed into the algorithm as input.
•
Encryption algorithm: The encryption algorithm performs various
transfor- mations on the plaintext.
•
Public and private
keys: This is a pair of keys that
have been selected so that if one
is used for encryption, the other is used for decryption. The exact
transfor- mations performed by the algorithm depend on the public or
private key that is provided
as input.
•
Ciphertext: This is the scrambled message
produced as output.
It depends on the
plaintext and the key. For a given
message, two different keys will produce two different ciphertexts.
•
Decryption algorithm: This algorithm accepts the ciphertext and the matching key and produces the original plaintext.
The essential steps are the following.
1.
Each user generates
a pair of keys to be used for the encryption and decryp- tion of messages.
2.
Each user places one of the two keys in a public register or other accessible file. This is the public
key. The companion key is kept private. As Figure 9.1a suggests, each user maintains a collection of public keys obtained
from others.
3.
If Bob wishes to send a confidential message to Alice,
Bob encrypts the message
using Alice’s public
key.
4.
When Alice receives
the message, she decrypts it using her private key. No other recipient can
decrypt the message because only Alice knows Alice’s private key.
With this approach, all participants have
access to public keys, and private keys are generated locally by each
participant and therefore need never be distrib- uted. As long as a user’s
private key remains protected and secret, incoming com- munication is secure. At any time, a system can change its private
key and publish the companion public
key to replace its old public key.
Table 9.2 summarizes some of the important aspects
of symmetric and public-
key encryption. To discriminate
between the two, we refer to the key used in
sym- metric encryption as a secret
key. The two keys used for asymmetric encryption are referred to as the public key and the private
key.2
Invariably, the private key is
kept secret, but it is referred to as a
private key rather than a secret key to avoid confusion with symmetric
encryption.
Let us take a closer look at the essential elements of a
public-key encryption scheme, using Figure 9.2 (compare with Figure 2.2). There
is some source A that

produces a message in plaintext, X = [X1, X2, . . . , XM].
The M elements of X are
letters in some finite alphabet. The message is intended for destination B. B gener- ates a related pair of keys: a public
key, PUb, and a private key, PRb. PRb is known only to B, whereas PUb is publicly
available and therefore
accessible by A.
With the message
X
and the encryption key PUb as input,
A forms
the ciphertext Y = [Y1, Y2, . . . , YN]:
Y = E(PUb, X)
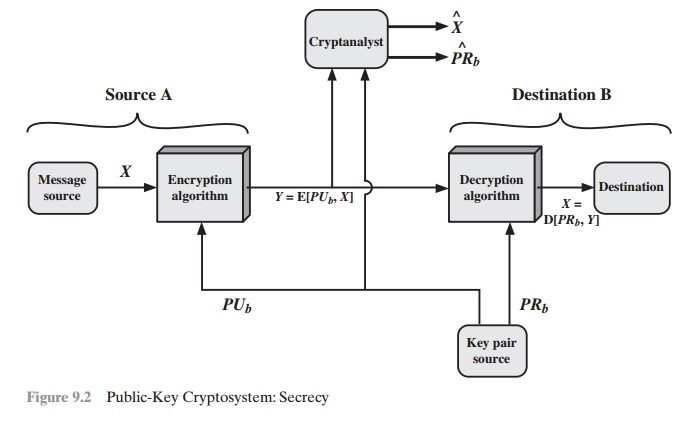
The intended receiver,
in possession of the matching
private key, is able to invert the
transformation
X
= D(PRb, Y)
An adversary, observing Y and having access to PUb, but not having access to PRb or X, must attempt to recover X and/or PRb. It is assumed that the adversary does have knowledge of the encryption (E) and decryption (D) algorithms. If the adver- sary is interested only in this particular message, then the focus of effort is to recover X by generating a plaintext estimate Xˆ. Often, however, the adversary is interested in being able to read future messages as well, in which case an attempt is made to recover PRb by generating an estimate PRˆ .
We mentioned earlier that either of the two related keys can be used for encryption, with the other
being used for decryption. This enables a rather different cryptographic scheme to be implemented.
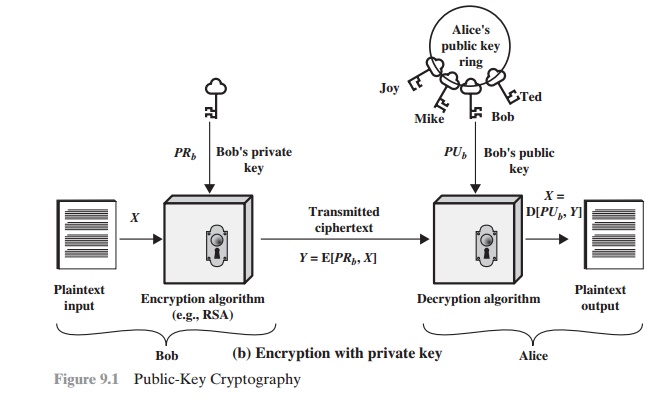
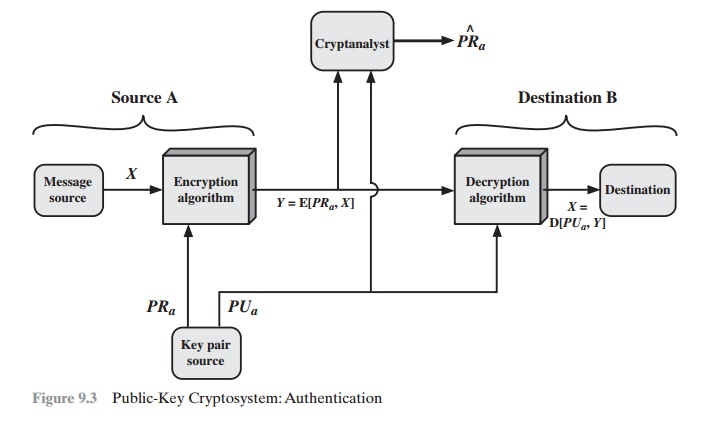
Whereas the scheme illustrated in Figure 9.2 provides
confidentiality, Figures 9.1b and 9.3 show the use of public-key
encryption to provide authentication:
Y = E(PRa, X) X
= D(PUa, Y)
In this case, A prepares a message to B and encrypts it
using A’s private key before
transmitting it. B can decrypt
the message using A’s public
key. Because the message
was encrypted using A’s private key, only A could have prepared
the message. Therefore, the entire encrypted message serves as a digital signature. In addition, it is impossible to alter the message without
access to A’s private key, so the message is authenticated both in terms of source and in terms of data integrity.
In the preceding
scheme, the entire message is encrypted, which, although validating both author and contents, requires a great
deal of storage. Each docu- ment must be kept in plaintext to be used for
practical purposes. A copy also must
be stored in ciphertext so that the origin and contents can be verified in case
of a dispute. A more efficient way of achieving the same results is to encrypt
a small block of bits that is a function
of the document. Such a block, called an authentica- tor, must have the property
that it is infeasible to change the document without changing the authenticator. If the authenticator is encrypted with the sender’s private key, it serves as a signature that
verifies origin, content, and sequencing. Chapter 13 examines this technique in detail.
It is important to emphasize that the encryption process depicted in Figures
9.1b and 9.3 does not provide
confidentiality. That is, the message being
sent is safe from
alteration but not
from eavesdropping. This is obvious
in the case
of a signature based on
a portion of the message, because the rest of the message is transmitted in the
clear. Even in the case of complete encryption, as shown in Figure 9.3, there
is no protection of confidentiality because any observer
can decrypt the message by using
the sender’s public key.
It is, however, possible
to provide both the authentication function and confi- dentiality by a double use of the public-key scheme (Figure 9.4):
Z = E(PUb, E(PRa, X))
X = D(PUa, D(PRb, Z))
In this case, we begin as before by encrypting a message, using the sender’s
private key. This provides the digital signature. Next, we encrypt
again, using the receiver’s
public key. The final ciphertext can
be decrypted only by the intended receiver, who
alone has the matching private key.
Thus, confidentiality is provided. The
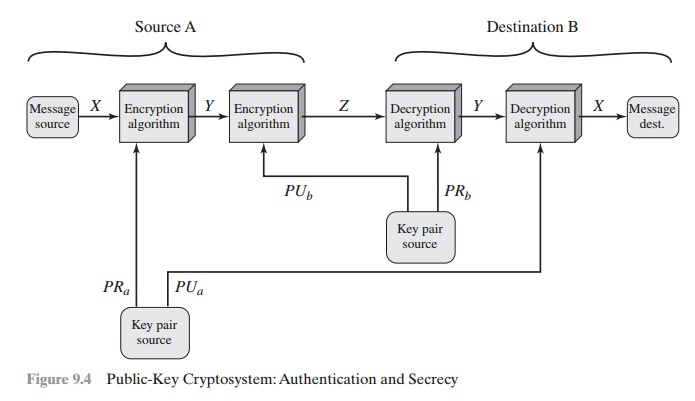
disadvantage of this approach is that the
public-key algorithm, which is complex, must be exercised four times rather
than two in each communication.
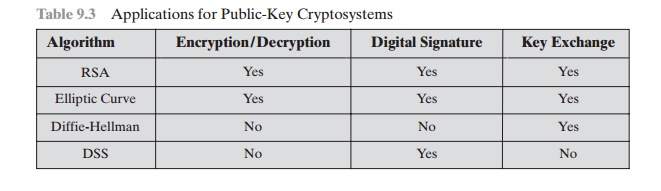
Applications for Public-Key Cryptosystems
Before proceeding, we need to clarify one aspect of public-key cryptosystems that is otherwise likely to lead to confusion. Public-key
systems are characterized by the use of a cryptographic algorithm with two keys, one held private and one avail- able
publicly. Depending on the application, the sender uses either the sender’s private
key or the receiver’s public key, or
both, to perform some type of crypto- graphic
function. In broad
terms, we can classify the use of public-key
cryptosystems into three categories
•
Encryption /decryption: The sender encrypts a message with the recipient’s public key.
•
Digital signature: The sender “signs”
a message with
its private key. Signing
is achieved by a cryptographic algorithm applied to the message or to a
small block of data that is a function
of the message.
•
Key exchange: Two sides cooperate to exchange a session key. Several
different approaches are possible, involving the private
key(s) of one or both parties.
Some algorithms are suitable for all three applications, whereas
others can be used only for one or two of these
applications. Table 9.3 indicates the applications supported by the algorithms discussed in this book.
Requirements for Public-Key Cryptography
The cryptosystem illustrated in Figures 9.2 through 9.4 depends on a cryptographic algorithm based on two
related keys. Diffie and Hellman postulated this system without demonstrating that such algorithms exist. However,
they did lay out the conditions that
such algorithms must
fulfill [DIFF76b].
1.
It is
computationally easy for a party B to generate a pair (public key PUb, private key PRb).
2.
It is
computationally easy for a sender A, knowing the public key and the message
to be encrypted, M, to generate
the corresponding ciphertext:
C = E(PUb, M)
Table 9.3 Applications
for Public-Key Cryptosystems
1.
It is computationally easy for the receiver B to decrypt the resulting
ciphertext using the private key
to recover the original message:
M = D(PRb, C) = D[PRb, E(PUb,
M)]
2.
It is computationally infeasible for an adversary, knowing the public
key, PUb, to determine the
private key, PRb.
3.
It is computationally infeasible for an adversary, knowing the public
key, PUb,
and a ciphertext, C, to recover
the original message,
M.
We can add a sixth requirement that, although useful, is not
necessary for all public-key applications:
4.
The two keys can be applied
in either order:
M = D[PUb, E(PRb, M)] = D[PRb, E(PUb,
M)]
These are formidable requirements, as
evidenced by the fact that only a few algorithms (RSA, elliptic curve cryptography, Diffie-Hellman, DSS) have received widespread acceptance in the several decades
since the concept
of public-key cryp- tography was proposed.
Before elaborating on why the requirements are
so formidable, let us first recast them.
The requirements boil down to the need for a trap-door
one-way func- tion. A one-way function3 is one that maps a
domain into a range such that every function value has a unique inverse, with
the condition that the calculation of the
function is easy, whereas the calculation of
the inverse is infeasible:
Y = f(X) easy
X = f- 1(Y) infeasible
Generally, easy is defined
to mean a problem that can be solved in polynomial
time as a function of input length. Thus, if
the length of the input is n bits, then the time to compute
the function is proportional to na, where
a
is a fixed
constant. Such algorithms
are said to belong to the class P. The term infeasible is a much fuzzier concept. In general, we can say a problem
is infeasible if the effort
to solve it grows
faster than polynomial time as a function
of input size. For example, if the length of
the input is n bits and the time to
compute the function is proportional to 2n,
the problem is considered infeasible. Unfortunately, it is difficult
to determine if a particular
algorithm exhibits this complexity. Furthermore, traditional notions of
computational complexity focus
on the worst-case or average-case complexity of an algorithm.
These measures are inadequate for cryptography, which requires that it be
infeasible to invert a function for virtually all inputs, not for the worst
case or even average case. A brief introduction to some of these concepts is
provided in Appendix 9B.
We now turn
to the definition of a trap-door one-way
function, which is easy to calculate in one direction and
infeasible to calculate in the other direction unless certain additional information is known. With the additional information the inverse
can be calculated in polynomial time. We can summarize as follows: A trap-
door one-way function is a family of invertible functions
fk, such that
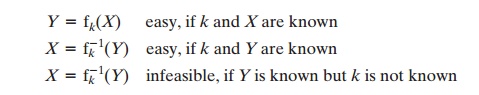
Thus, the development of a practical public-key scheme depends
on discovery of a
suitable trap-door one-way
function.
Public-Key Cryptanalysis
As with symmetric encryption, a public-key
encryption scheme is vulnerable to a brute-force attack. The countermeasure is the same:
Use large keys. However,
there is a tradeoff
to be considered. Public-key systems
depend on the use of some sort of
invertible mathematical function. The complexity of calculating these
functions may not scale linearly with the number of bits in the key but grow more rapidly than that.
Thus, the key size must be large enough to make brute-force attack impractical but small
enough for practical encryption and
decryption. In practice, the key sizes that have been proposed do make brute-force attack impractical but result
in encryption/decryption speeds
that are too slow for general-purpose use. Instead, as was mentioned earlier,
public-key encryption is currently confined to key man- agement and signature applications.
Another form of attack is to find some way
to compute the private key given the
public key. To date, it has
not been mathematically proven that this form
of attack is infeasible for a particular public-key algorithm. Thus, any given algorithm, including the widely used RSA
algorithm, is suspect. The history of cryptanalysis shows that a problem that
seems insoluble from one perspective can be found to have a solution if looked at in an entirely different way.
Finally, there is a form of attack that is peculiar to public-key systems.
This is, in essence, a probable-message attack. Suppose, for example,
that a message were to be sent that consisted solely of a 56-bit DES key. An adversary
could encrypt all possible 56-bit DES keys using the
public key and could discover the encrypted key by matching the transmitted ciphertext. Thus, no matter how large the key size of the public-key scheme, the attack
is reduced to a brute-force attack on a 56-bit key. This attack can be thwarted by appending some random bits to
such simple messages.
Related Topics