Chapter: Transmission Lines and Waveguides : Waveguides and Cavity Resonators
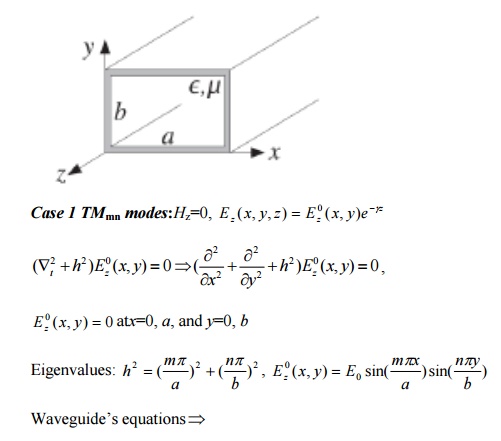
TM and TE waves in Rectangular wave guides
TM and TE waves in Rectangular wave guides
• For a rectangular waveguide. a) The dominant mode is TE01
• For a circular waveguide, b) The dominant mode is TE11

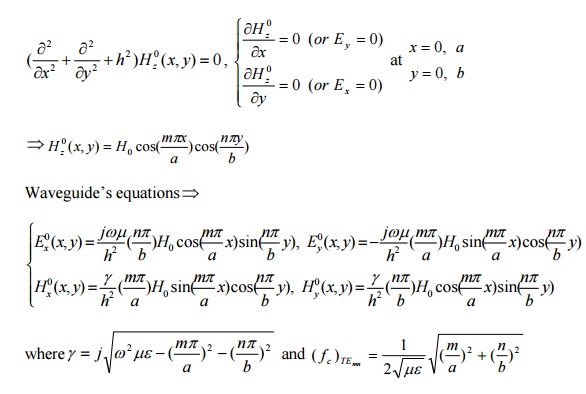

Example 2: An air-filled a×b (b<a<2b) rectangular waveguide is to be constructed to operate at 3GHz in the dominant mode. We desire the operating frequency to be at least 20% higher than the cutoff frequency of the dominant mode and also at least 20% below the cutoff frequency of the next higher-order mode. (a) Give a typical design for the dimensions a and b. (b) Calculate for your design β, vp, λg and the wave impedance at the operating frequency. (Sol)
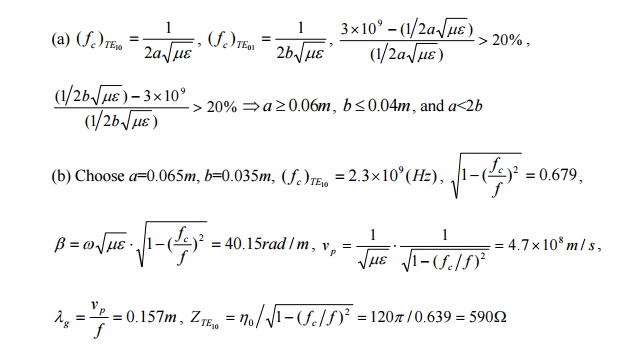
Example 3: A 3cm×1.5cm rectangular waveguide operating at 6GHz has a dielectric discontinuity between medium 1 (µ0,ε0) and medium 2 (µ0,4ε0). (a) Find the SWR in the free-space region. (b) Find the length and the permittivity of a quarter wave section to achieve a match between two media.
(Sol.)

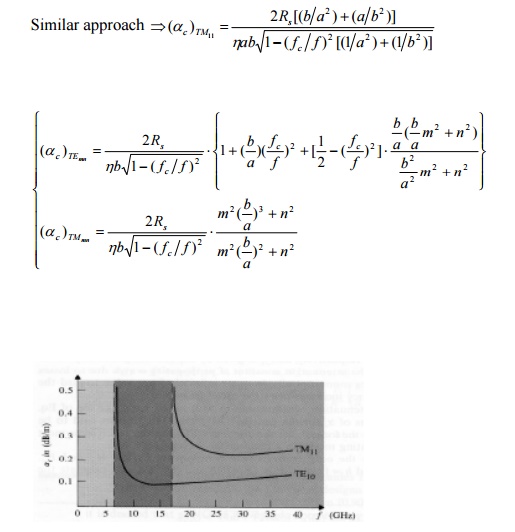
Example 4: Write the instantaneous field expressions for the TM11 mode in a rectangular waveguide of sides a and b. (b) Sketch the electric and magnetic field lines in a typical xy-plane and in a typical yz-plane. (c) Attenuation of the rectangular waveguide
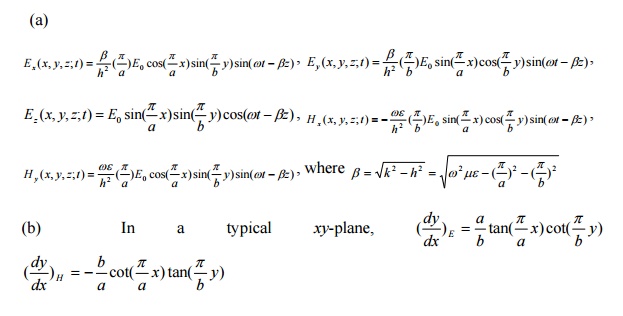

Example 5: A TE10 wave at 10GHz propagates in a brass σc=1.57×107(S/m) rectangular waveguide with inner dimensions a=1.5cm and b=0.6cm, which is filled with εr=2.25, µr=1, loss tangent=4×10-4. Determine (a) the phase constant, (b) the guide wavelength, (c) the phase velocity, (d) the wave impedance, (e) the attenuation constant due to loss in the dielectric, and (f) the attenuation constant due to loss in the guide walls.
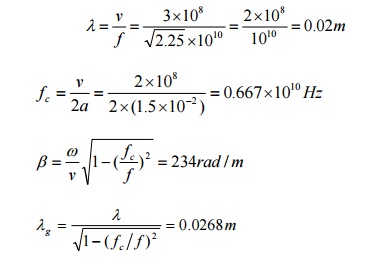
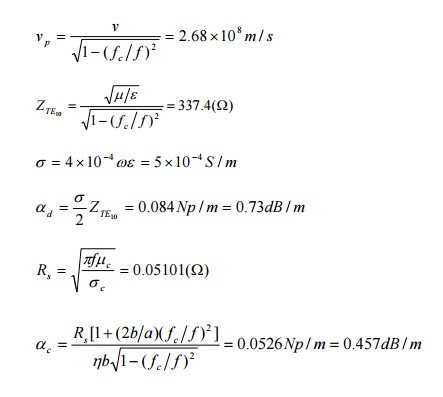
Example 6: An air-filled rectangular waveguide made of copper and having transverse dimensions a=7.20cm and b=3.40cm operates at a frequency 3GHz in the dominant mode. Find (a) fc, (b) λg, (c) αc, and (d) the distance over which the field intensities of the propagating wave will be attenuated by 50%.
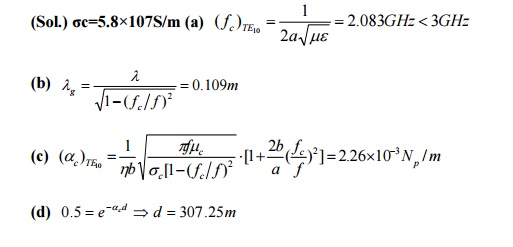
Example 7: An average power of 1kW at 10GHz is to be delivered to an antenna at the TE10 mode by an air-filled rectangular copper waveguide 1m long and having sides a=2.25cm and b=1.00cm. Find (a) the attenuation constant due to conductor losses, (b) the maximum values of the electric and magnetic field intensities within the waveguide, (c) the maximum value of the surface current density on the conducting walls, (d) the total amount of average power dissipated in the waveguide.
(Sol.)
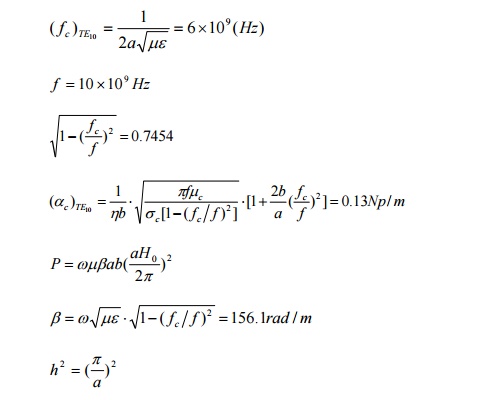
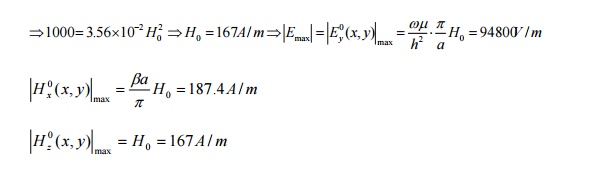
If at input end, all factor×e0.13 (=1.138)
Related Topics