Chapter: Transmission Lines and Waveguides : Waveguides and Cavity Resonators
Rectangular and circular cavity resonators
Rectangular and circular cavity resonators
Resonator is a tuned circuit which resonates at a particular frequency at which the energy stored in the electric field is equal to the energy stored in the magnetic field.
Resonant frequency of microwave resonator is the frequency at which the energy in the resonator attains maximum value. i.e., twice the electric energy or magnetic energy.
At low frequencies upto VHF (300 MHz), the resonator is made up of the reactive elements or the lumped elements like the capacitance and the inductance.
The inductance and the capacitance values are too small as the frequency is increased beyond the VHF range and hence difficult to realize.
Transmission line resonator can be built using distributed elements like sections of coaxial lines. The coaxial lines are either opened or shunted at the end sections thus confining the electromagnetic energy within the section and acts as the resonant circuit having a natural resonant frequency.
At very high frequencies transmission line resonator does not give very high quality factor Q due to skin effect and radiation loss. So, transmission line resonator is not used as microwave resonator.
The performance parameters of microwave resonator are:
(i) Resonant frequency
(ii)Quality factor
(iii) Input impedance
Quality Factor of a Resonator.:
• The quality factor Q is a measure of frequency selectivity of the resonator.
• It is defined as Q = 2 x Maximum energy stored / Energy dissipated per cycle = W / P
Where,
a. W is the maximum stored energy
b. P is the average power loss
The methods used for constructing a resonator:
The resonators are built by,
a)Using lumped elements like L and C
b) Using distributed elements like sections of coaxial lines
c) Using rectangular or circular waveguide
There are two types of cavity resonators.
a)Rectangular cavity resonator
b)Circular cavity resonator
Rectangular or circular cavities can be used as microwave resonators because they have natural resonant frequency and behave like a LCR circuit.
Cavity resonator can be represented by a LCR circuit as:
• The electromagnetic energy is stored in the entire volume of the cavity in the form of electric and magnetic fields.
• The presence of electric field gives rise to a capacitance value and the presence of magnetic field gives rise to a inductance value and the finite conductivity in the walls gives rise to loss along the walls giving rise to a resistance value.
• Thus the cavity resonator can be represented by a equivalent LCR circuit and have a natural resonant frequency.
* Cavity resonators are formed by placing the perfectly conducting sheets on the rectangular or circular waveguide on the two end sections and hence all the sides are surrounded by the conducting walls thus forming a cavity.
* The electromagnetic energy is confined within this metallic enclosure and they acts as resonant circuits.

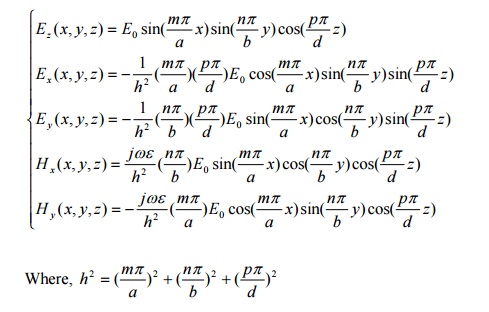

Note:TE101 mode is the dominant mode of the rectangular resonator in case of a>b<d.
Circular Cavity Resonators:
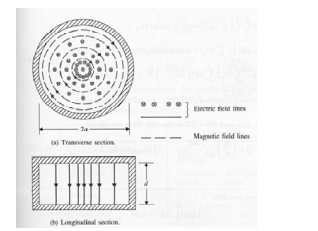
For an air-filled circular cylindrical cavity resonator of radius a and length d. The resonant frequencies are,
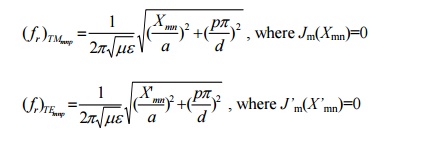
In case of 2d>2a>d, the dominant mode of the circular cylindrical cavity is TM010 mode:

Excitations of Waveguides

The basic configurations of coaxial resonators are:
a) Quarter wave coaxial cavity b) Half wave coaxial cavity c) Capacitance end coaxial cavity
The dominant mode of a rectangular resonator depends on the dimensions of the cavity. For, b<a<d, the dominant mode is TE101.
The dominant mode of a circular resonator depends on the dimensions of the cavity.
For, d < 2a, the dominant mode is TM010.
Problem: A hollow circular cylindrical cavity resonator is to be constructed of copper such that its length d equals its diameter 2a. (a) Determine a and d for a resonant frequency of 10GHz at the TM010 mode. (b) Find the Q of the cavity at resonance.
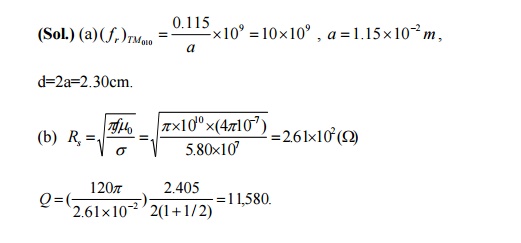
Related Topics