Structural Analysis: Finite Element Method

FINITE ELEMENT METHOD

1 INTRODUCTION

There are two version of FEM:

1.  Flexibility Method or Force Method

2.  Stiffness Method or Displacement Method.

·   The set of equations in the stiffness method are the equilibrium equations relating displacements of points.

·   Rayleigh- Ritzisan approximate method based on energy principle by

Which we can obtain equilibrium equations in matrix form.

1 IMPORTANT DEFINITION

Nodes are points on the structure at which displacements and rotations are to be found or prescribed.

Element is a small domain on which we can solve the boundary value problem in terms of the displacements and forces of the nodes on the element.

The discrete representation of the structure geometry by elements and nodes is called a mesh.

The process of creating a mesh (discrete entities) is called discretization.

Inter polation function isakinematicallyadmissible displacement function defined on an element that can be used for interpolating displacement values between the nodes.

The mesh, boundary conditions, loads, and material properties representing the actual structure is called a model.

Element stiffness matrix relate the displacements to the forcesat the element nodes.

Global stiffness matrix is an assembly of element stiffness matrix that relates the displacements of the nodes on the mesh to applied external forces.

1.2.Stepsin FEM procedure

1.Obtain element stiffness and element load vector.

2.Transform from local orientation to global orientation.

3.Assemble the global stiffness matrix and load vector.

4.Incorporate the external loads

5.Incorporate the boundary conditions.

6.Solve the algebraic equations for nodal displacements.

7.Obtain reaction force, stress, internal forces, strain energy.

8.Interpret and check the results.

9.Refinemeshif necessary, and repeat the above steps.

2.DISCRETISATION OF STRUCTURE

Discretization is the process of separating the length, area or volume we want to analyze into discrete (or separate) parts or elements.

3.DISPLACEMENT FUNCTIONS

The continuum is separated by imaginary lines or surfaces into a number of finite element

·        The elements are assumed to be connected at discrete number of nodal points situated on their boundaries.

·        Generalized displacements are the basic unknowns.

·        A function uniquely defines displacement field in terms of nodal displacements.

·        Compatibility between elements.

·        2D - 3D elasticity problems, displacement compatibility.

·        Plates and shells, displacements and their partial derivatives.

·        All possible rigid body displacements included (if not will not converge).

·     All uniform strain states included. The displacement function, uniquely defines

strain within an element in terms of nodal displacements.

These strains with any initial strain, together with elastic properties define the stress state.

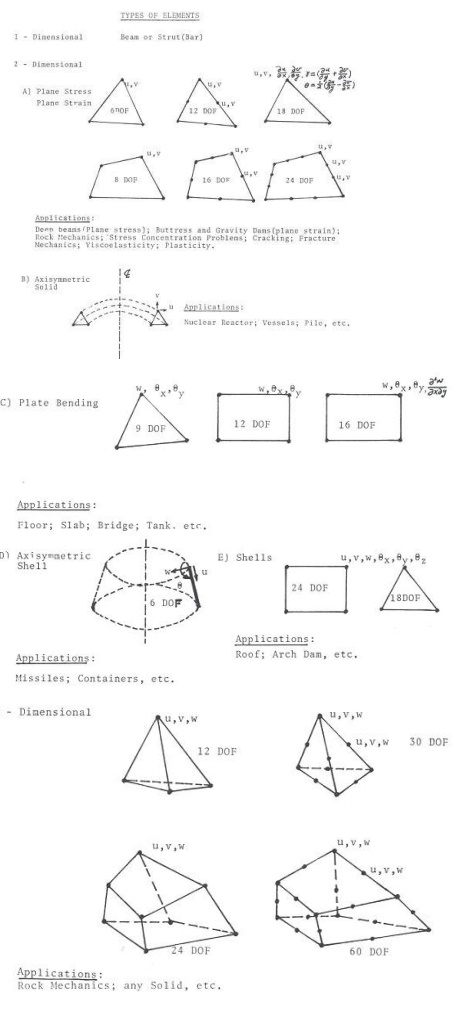
4 TYPES OF ELEMENT

Three are three types of elements are available.

·        1D Elements

·        2D Elements

·        3D Elements

4.1 1D Elements (Beam Element)

A beam can be approximated as a one dimensional structure. It can be split into one dimensional beam elements. So also, a continuous beam or a flexure frame can be discretized using 1D beam elements.

A pin jointed truss is readily made up of discrete 1D ties which are duly assembled.

4.2 2 D Elements (Triangular Element)

A plane wall ,plate, diaphragm, slab, shell etc., can be approximated as an assemblage of 2D elements. Triangular elements are the most used ones. when our 2D domain has curved boundaries it may be advantageous to choose elements that can have curved boundaries.

4.3 3 D Elements (Truss Element)

Analysis of solid bodies call for the use of 3 D elements. These have the drawback that the visualizations is complex. The size of the stiffness matrix to be handled can become enormous and unwieldy.

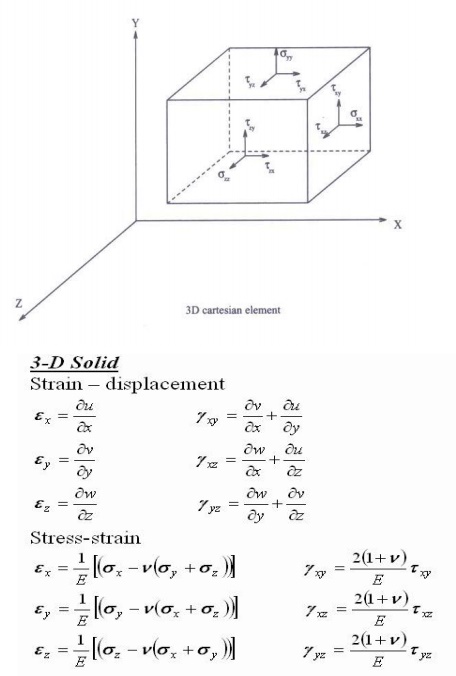
5 PLANE STRESS AND PLANE STRAIN

The plane stress problem is one in which two dimensions ,length and breadth are comparable and thickness dimension is very small (less than 1/10).Hence normal stress ?₂ and shear stresses ?_xz,?_yzare zero.

{? }= [D]{e }

[D]=Stress strain relationship matrix (or) constitutive matrix for plane stress problems. We have seen that in the Z direction the dimension of the plate in the plane stress

problem is very small. In plane strain problem, on the contrary the structure is infinitely long in

the Z direction. Moreover the boundary and body forces do not vary in the Z directions.

{? }= [D]{e }

[D]=Stress strain relationship matrix (or) constitutive matrix for plane strain problems.

FINITE ELEMENT METHOD

1. What is meant by Finite element method?

Finite element method (FEM)is a numerical technique for solving boundary value problems in which a large domain is divided into smaller pieces or elements. The solution is determined by asuuming certain ploynomials. The small pieces are called finite element and the polynomials are called shape functions.

2. List out the advantages of FEM.

·       Since the properties of each element are evaluated separately differnt material properties can be incorporated for each element.

·       There is no restriction in the shape of the medium.

·       Any type of boundary condition can be adopted.

3. List out the disadvantages of FEM.

·The computational cost is high.

·The solution is approximate and several checks are required.

4. Mention the various coordinates in FEM.

·       Local or element coordinates

·       Natural coodinates

·       Simple natural coodinates

·       Area coordiantesor Triangular coordiantes

·       Generalised coordinates

5. What are the basic steps in FEM?

·       Discretization of the structure

·       Selection of suitable displacement fuction

·       Finding the element properties

·       Assembling the element properties

·       Applying the boundary conditions

·       Solving the system of equations

·       Computing additional results

6. What is meant by discretization?

Discretization is the process of subdividing the given body into a number of elements which results in a system of equivalent finite elements.

7. What are the factors governing the selection of finite elements?

·The geometry of the body

·The number of independent space coordinates

·The nature of stress variation expected

8. Define displacement function.

Displcement function is defined as simple functions which are assumed to approximate the displacements for each element. They may assumed in the form of poynomials, or trignometrical functions.

9. Briefly explain a few terminology used in FEM.

The various terms used in FEM are explained below.

·        Finite element-Small elements used for subdividing the given domain tobe  analysed are called finite elements. The seelements may be 1D, 2D or 3D elements depend in on the type of structure.

·        Nodes and nodal points- The intersection of the differnt sides of elements are called nodes. Nodes are of two types - external nodes and internal nodes.

O External nodes - The nodal point connecting adjacent elements.

O Internal nodes- The extra nodes used to increase the accuracy of solution.

·          Nodal lines - The interface between elements are called nodal lines.

·           Continuum- The domain in which matter exists at every point is called a continuum. It can be assumed as having infinite number of connected particles.

·           Primary unknowns- The main unknowns involved in the formulation of the element properties are known as primary unknowns.

·           Secondary unknowns- These unknowns are derived from primary unknowns are known as secondary unknowns. In displacement formulations, displacements are treated as primary unknowns and stress, strain, moments and shear force are treated as secondary unknowns.

10.            What are differnt types of elements used in FEM?

The various elements used in FEM are classified as:

·       One dimensional elements(1D elements)

·       Two dimensional elements(2D elements)

·       Three dimensional elements(3D elements)

11.            Whatare1-D elements? Give examples.

Elements having a minimum of two nodes are called 1D elements. Beams are usually approximated with 1Delements. These may be straight or curved. There can be additional nodes within the element.

12.            Whatare2-D elements? Give examples.

A plane wall, plate, diaphragm, slab, shell etc. can be approximated as an assemblage of 2-D elements. Most commonly used elements are triangular, rectangular and quadrilateral elements.

13.            What are 3-D elements? Give examples.

3-D elements are used for modeling solid bodies and the various 3-Delements are tetrahedron, hexa hedron, and curved rectangular solid.

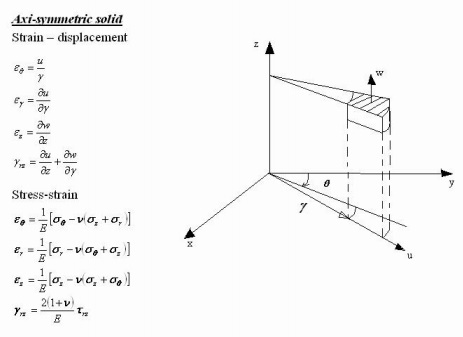
14.            What are axisymmetric elements?

Axisymmetric elements are obtained by rotatinga1-D line about an axis. Axisymmetric elements are shown in the figure below.

15.            Define Shape function.

Shape function is also called an approximate function or an interpolation function whose value is equal to unity at the node considered and zeros at all other nodes. Shape function is represented by Ni where i =nodeno.

16.            What are the properties of shape functions?

The properties of shape functions are:

·       Theno of shape functions will be equal to theno of nodes present in the element.

·        Shape function will have a unit value at the node considered and zero value at other nodes.

·       The sum of all the shape function is equal to 1. i. e. SNi =1

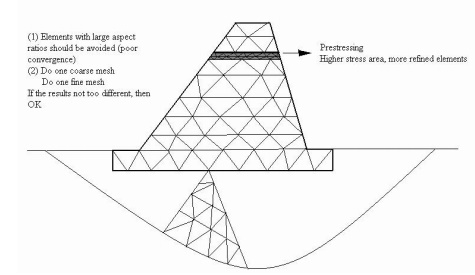
17.            Define aspect ratio.

Element aspect ratio is defined as the ratio of the largest dimension of the element to its smallest dimension.

18.            What are possible locations for nodes?

The possible locations for nodes are:

·Point of application of concentrated load.

·Location where there is a change in intensity of loads

·Locations where there are discontinuities in the geometry of the structure

·Interfaces between materials of different properties.

19.            What are the characteristics of displacement functions?

Displacement functions should have the following characteristics:

The displacement field should be continuous.

·       The displacement function should be compatible between adjacent elements

·       The displacement field must represent constant strain states of elements

·        The displacement function must represent rigid body displacements of an element.

20.            What is meant by plane strain condition?

Plane strain is a state of strain in which normal strain and shear strain directed perpendicular to the plane of body is assumed to be zero.