Chapter: Control Systems : State Variable Analysis
State space representation for discrete time systems
State space representation for
discrete time systems
The
dynamics of a linear time (shift)) invariant discrete-time system may be
expressed in terms state (plant) equation and output (observation or
measurement) equation as follows
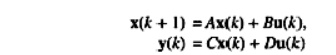
Where
x(k) an n dimensional slate rector at time t =kT. an r-dimensional control
(input) vector y(k). an m-dimensional output vector ,respectively, are
represented as
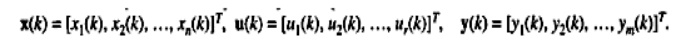
The
parameters (elements) of A, an nX n
(plant parameter) matrix. B an nX r control (input) matrix, and C An m X r
output parameter, D an m X r parametric matrix are constants for the LTI
system. Similar to above equation state variable representation of SISO (single
output and single output) discrete-rime system (with direct coupling of output
with input) can be written as
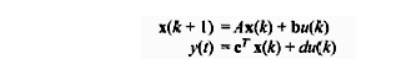
Where the
input u, output y and d. are scalars, and b and c are n-dimensional vectors.
The concepts of controllability and observability for discrete time system are
similar to the continuous-time system. A discrete time system is said to be
controllable if there exists a finite integer n and input mu(k); k [0,n
1] that will transfer any state (0) x0
= bx(0) to the state xn at k = n n.
Related Topics