Solution of State equations

Solution of State equations

Consider the state equation n of linear time invariant system as,

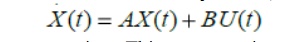
The matrices A and B are constant matrices. This state equation can be of two types,

1. Homogeneous and

2. Non homogeneous

Homogeneous Equation

If A is a constant matrix and input control forces are zero then the equation takes the form,

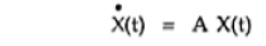
Such an equation is called homogeneous equation. The obvious equation is if input is zero, In such systems, the driving force is provided by the initial conditions of the system to produce the output. For example, consider a series RC circuit in which capacitor is initially charged to V volts. The current is the output. Now there is no input control force i.e. external voltage applied to the system. But the initial voltage on the capacitor drives the current through the system and capacitor starts discharging through the resistance R. Such a system which works on the initial conditions without any input applied to it is called homogeneous system.

Non homogeneous Equation

If A is a constant matrix and matrix U(t) is non-zero vector i.e. the input control forces are applied to the system then the equation takes normal form as,

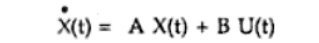
Such an equation is called non homogeneous equation. Most of the practical systems require inputs to dive them. Such systems arc non homogeneous linear systems. The solution of the state equation is obtained by considering basic method of finding the solution of homogeneous equation.