Sorting Techniques

Sorting Techniques

Bubble sort algorithm

Bubble sort is a simple sorting algorithm. The algorithm starts at the beginning of the list of values stored in an array. It compares each pair of adjacent elements and swaps them if they are in the unsorted order. This comparison and passed to be continued until no swaps are needed, which indicates that the list of values stored in an array is sorted. The algorithm is a comparison sort, is named for the way smaller elements "bubble" to the top of the list. Although the algorithm is simple, it is too slow and less efficient when compared to insertion sort and other sorting methods.

Assume list is an array of n elements. The swap function swaps the values of the given array elements.

Pseudo code

1. Start with the first element i.e., index = 0, compare the current element with the next element of the array.

2. If the current element is greater than the next element of the array, swap them.

3. If the current element is less than the next or right side of the element, move to the next element. Go to Step 1 and repeat until end of the index is reached.

Let's consider an array with values {15, 11, 16, 12, 14, 13} Below, we have a pictorial representation of how bubble sort will sort the given array.

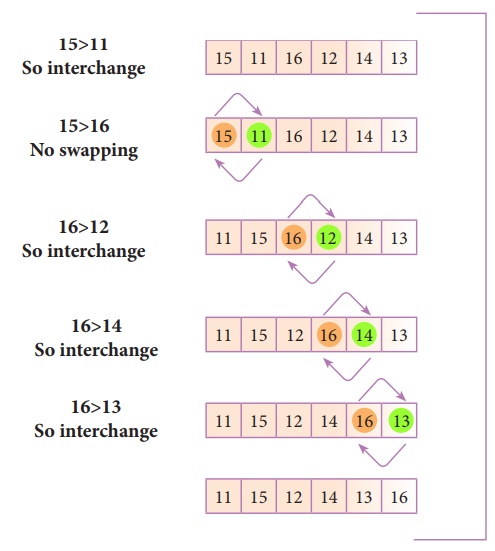
The above pictorial example is for iteration-1. Similarly, remaining iteration can be done. The final iteration will give the sorted array.

At the end of all the iterations we will get the sorted values in an array as given below:

Selection sort

The selection sort is a simple sorting algorithm that improves on the performance of bubble sort by making only one exchange for every pass through the list. This algorithm will first find the smallest elements in array and swap it with the element in the first position of an array, then it will find the second smallest element and swap that element with the element in the second position, and it will continue until the entire array is sorted in respective order.

This algorithm repeatedly selects the next-smallest element and swaps in into the right place for every pass. Hence it is called selection sort.

Pseudo code

1. Start from the first element i.e., index-0, we search the smallest element in the array, and replace it with the element in the first position.

2. Now we move on to the second element position, and look for smallest element present in the sub-array, from starting index to till the last index of sub - array.

3. Now replace the second smallest identified in step-2 at the second position in the or original array, or also called first position in the sub array.

4. This is repeated, until the array is completely sorted.

Let's consider an array with values {13, 16, 11, 18, 14, 15}

Below, we have a pictorial representation of how selection sort will sort the given array.

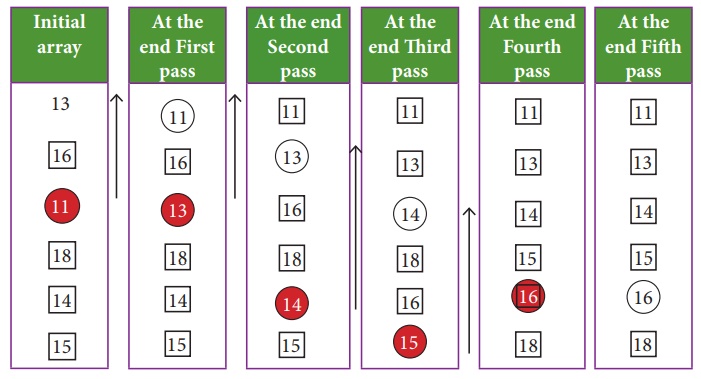
In the first pass, the smallest element will be 11, so it will be placed at the first position.

After that, next smallest element will be searched from an array. Now we will get 13 as the smallest, so it will be then placed at the second position.

Then leaving the first element, next smallest element will be searched, from the remaining elements. We will get 13 as the smallest, so it will be then placed at the second position.

Then leaving 11 and 13 because they are at the correct position, we will search for the next smallest element from the rest of the elements and put it at third position and keep doing this until array is sorted.

Finally we will get the sorted array end of the pass as shown above diagram.

Insertion sort

Insertion sort is a simple sorting algorithm. It works by taking elements from the list one by one and inserting then in their correct position in to a new sorted list. This algorithm builds the final sorted array at the end. This algorithm uses n-1 number of passes to get the final sorted list as per the pervious algorithm as we have discussed.

Pseudo for Insertion sort

Step 1 − If it is the first element, it is already sorted.

Step 2 − Pick next element

Step 3 − Compare with all elements in the sorted sub-list

Step 4 − Shift all the elements in the sorted sub-list that is greater than the value to be sorted

Step 5 − Insert the value

Step 6 − Repeat until list is sorted

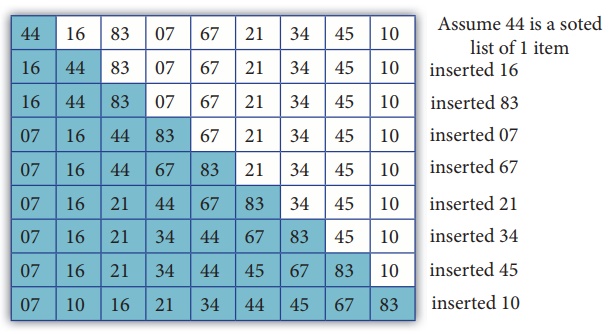
At the end of the pass the insertion sort algorithm gives the sorted output in ascending order as shown below: