Chapter: Power System Analysis : Stability Analysis
Single Machine Infinite Bus (SMIB) System: Development of Swing Equation
SINGLE MACHINE INFINITE BUS (SMIB) SYSTEM: DEVELOPMENT OF SWING EQUATION.
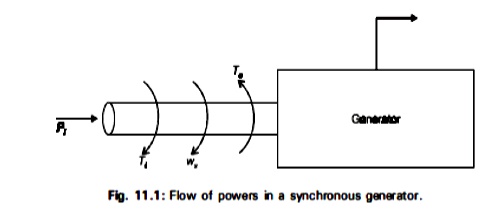
Consider a synchronous generator developing an electromagnetic torque Te (and a corresponding electromagnetic power Pe) while operating at the synchronous speed ωm. I the input torque provided by the prime mover at the generator shaft is Ti, then under steady state conditions (with no disturbance).
Te = Ti …. (11.10)
Here we have neglected any retarding torque due to rotational losses. Therefore we have

If there is a departure from steady state occurs, or example, a change in load or a fault, then input power Pi is not equal to Pe if the armature resistance is neglected. Therefore let-side of eqn. (11.12) is not zero and an accelerating torque comes into play. If Pa is the corresponding accelerating (or decelerating) power, then
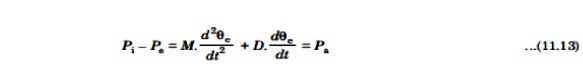
Where M has been defined in eqn. (11.8) or eqn. (11.9). D is a damping coefficient and qe is the electrical angular position o the rotor. It is more convenient to measure the angular position o the rotor with respect to a synchronously rotating frame of reference. Let

Where δ is the power angle of the synchronous machine. Neglecting damping (i.e., D=0) and substituting eqn. (11.15) in eqn. (11.13), we get,

Eqn. (11.20) is called swing equation. It describes the rotor dynamics for a synchronous machine. Although damping is ignored but it helps to stabilizer the system. Damping must be considered in dynamic stability study.
A 400 MVA synchronous machine has H1=4.6 MJ/MVA and a 1200 MVA machines H2=3.0 MJ/MVA. Two machines operate in parallel in a power plant. Find out Heq relative to a 100MVA base.

A 100 MVA, two pole, 50Hz generator has moment of inertia 40 x 103 kg-m2.what is the energy stored in the rotor at the rated speed? What is the corresponding angular momentum? Determine the inertia constant h.

The sending end and receiving end voltages of a three phase transmission line at a 200MW load are equal at 230KV.The per phase line impedance is j14 ohm. Calculate the maximum steady state power that can be transmitted over the line.
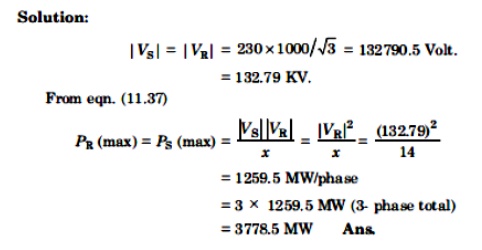
Equal area criterion in transient stability.
Solution o swing equation is not always necessary to investigate the system stability. Rather, in some cases, a direct approach may be taken. Such an approach is based on the equal-area criterion.
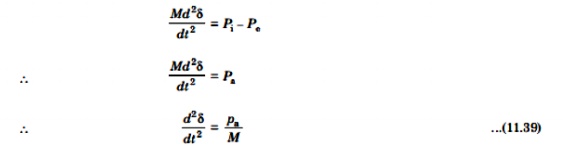
As is shown in Fig 11.6, in an unstable system, δ increases indefinitely with time and machine some synchronism. In a stable system, δ undergoes oscillations, which eventually die out to damping. From Fig.11.6, it is clear that, for a system to be stable, it must be that
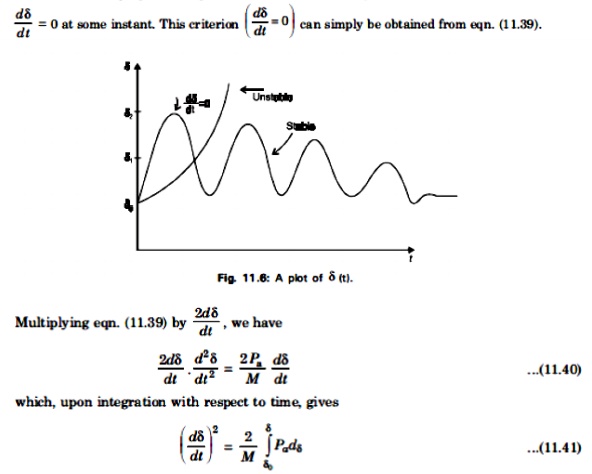

This condition requires that, for stability, the area under the graph of accelerating power Pa versus δ must be zero for some value of δ; that is, the positive(or accelerating) area under the graph must be equal to the negative (or decelerating) area. This criterion is therefore known as the equal-area criterion for stability and it is shown in ig. 11.7.
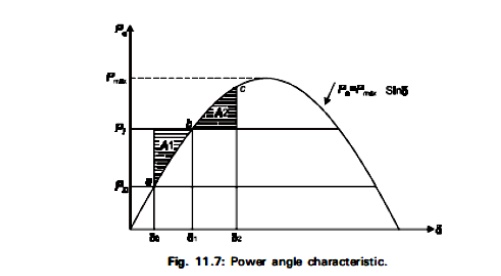
In Fig 11.7, point ‘a’ corresponding to the δo is the initial steady state operating point. At this point, the input power to the machine, Pi0 = Pe0 is the developed power. When a sudden increase in shat input power occurs to Pi , the accelerating power, Pa, becomes positive and the rotor moves towards point ‘b’. We have assumed that the machine is connected to a large power system so that |Vt| does not charge and also that xd does not charge and that a constant ield current maintains |Eg| constant. Consequently, the rotor accelerates.

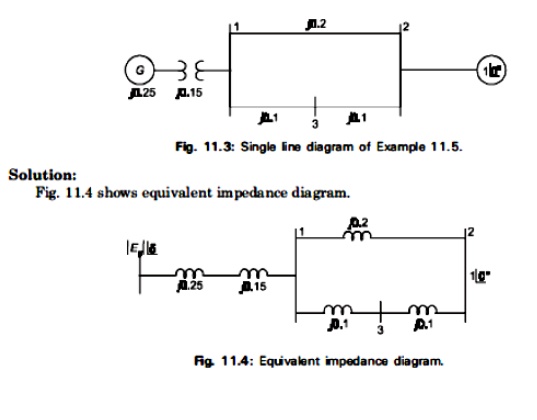
A single line diagram of a system is shown in fig. All the values are in per unit on a common base. The power delivered into bus 2 is 1.0 p.u at 0.80 power factor lagging. Obtain the power angle equation and the swing equation for the system. Neglect all losses.
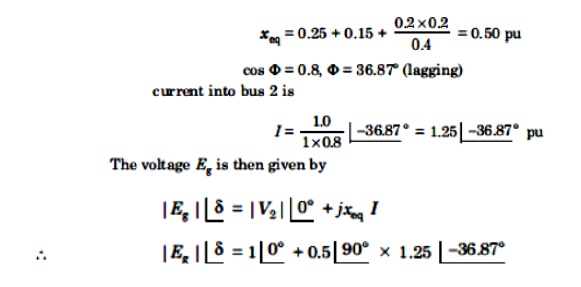
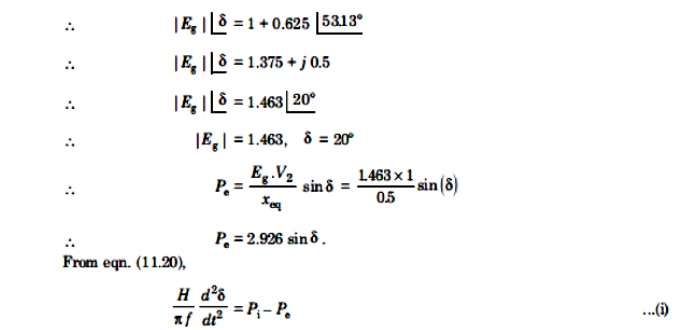

Related Topics