Chapter: Digital Communication : Sampling & Quantization
Sampling theorem for Low pass signals
SAMPLING:
A message
signal may originate from a digital or analog source. If the message signal is
analog in nature, then it has to be converted into digital form before it can
transmit by digital means. The process by which the continuous-time signal is
converted into a discrete–time signal is called Sampling. Sampling operation is
performed in accordance with the sampling theorem.
SAMPLING THEOREM FOR LOW-PASS
SIGNALS:-
Statement:
- “If a band –limited signal g(t) contains no frequency components for ׀f׀ >
W, then it is completely described by instantaneous values g(kTs) uniformly
spaced in time with period Ts ≤ 1/2W. If the sampling rate, fs is equal to the
Nyquist rate or greater (fs ≥ 2W), the signal g(t) can be exactly
reconstructed.
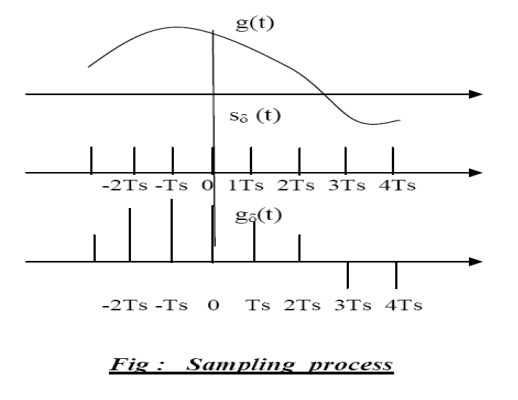
Proof:- Part - I If a signal x(t) does
not contain any frequency component beyond W Hz, thenthe signal is completely
described by its instantaneous uniform samples with sampling interval (or
period ) of Ts< 1/(2W) sec.
Part – II
The signal x(t) can be accurately reconstructed (recovered) from the set of
uniform instantaneous samples by passing the samples sequentially through an
ideal (brick-wall) lowpass filter with bandwidth B, where W ≤ B <fs – W and
fs = 1/(Ts).
If x(t)
represents a continuous-time signal, the equivalent set of instantaneous
uniform samples {x(nTs)} may be represented as,

where
x(nTs) = x(t)⎢t =nTs ,
δ(t) is a unit pulse singularity function and „n‟ is an integer.The
continuous-time signal x(t) is multiplied by an (ideal) impulse train to obtain
{x(nTs)} and can be rewritten as,

Now, let
X(f) denote the Fourier Transform F(T) of x(t), i.e.
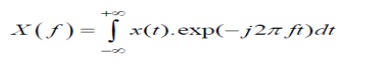
Now, from
the theory of Fourier Transform, we know that the F.T of Σ δ(t- nTs), the impulse
train in time domain, is an impulse train in frequency domain:
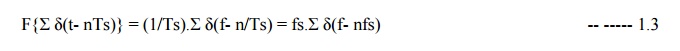
If Xs(f)
denotes the Fourier transform of the energy signal xs(t), we can write using
Eq. (1.2.4) and the convolution property:
Xs(f) =
X(f)* F{Σ δ(t- nTs)}
X(f)*[fs.Σ
δ(f- nfs)]
= fs.X(f)*Σ
δ(f- nfs)
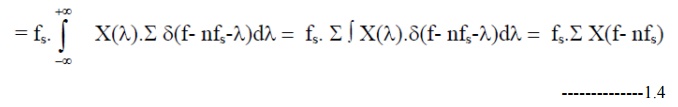
Related Topics