Aliasing and signal reconstruction

Aliasing and signal reconstruction:

Nyquist‟s theorems as stated above and also helps to appreciate their practical implications.

Let us note that while writing Eq.(1.4), we assumed that x(t) is an energy signal so that its Fourier transform exists. With this setting, if we assume that x(t) has no appreciable frequency component greater than W Hz and if fs> 2W, then Eq.(1.4) implies that Xs(f), the Fourier Transform of the sampled signal X_s(t) consists of infinite number of replicas of X(f), centered at discrete frequencies n.fs, -∞ < n < ∞ and scaled by a constant fs= 1/Ts.

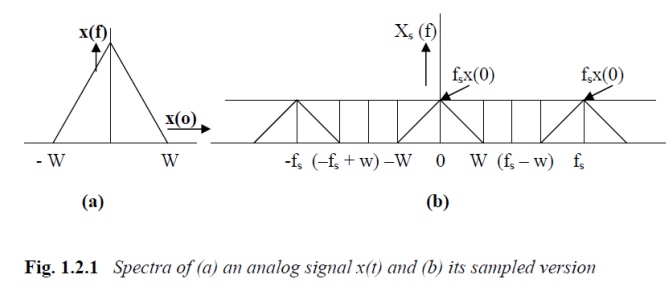
Fig. 1.2.1 indicates that the bandwidth of this instantaneously sampled wave xs(t) is infinitewhile the spectrum of x(t) appears in a periodic manner, centered at discrete frequency values n.fs. Part – I of the sampling theorem is about the condition fs> 2.W i.e. (fs – W) > W and (– fs + W) < – W. As seen from Fig. 1.2.1, when this condition is satisfied, the spectra of xs(t), centered at f = 0 and f = ± fs do not overlap and hence, the spectrum of x(t) is present in xs(t) without any distortion. This implies that xs(t), the appropriately sampled version of x(t), contains all information about x(t) and thus represents x(t).

The second part suggests a method of recovering x(t) from its sampled version xs(t) by using an ideal lowpass filter. As indicated by dotted lines in Fig. 1.2.1, an ideal lowpass filter (with brick-wall type response) with a bandwidth W ≤ B < (fs – W), when fed with xs(t), will allow the portion of Xs(f), centered at f = 0 and will reject all its replicas at f = n fs, for n ≠ 0. This implies that the shape of the continuous time signal xs(t), will be retained at the output of the ideal filter.