Chapter: Mechanical : Gas Dynamics and Jet Propulsion : Space Propulsion
Rocket Propulsion
Rocket Propulsion
In the section about the rocket equation we explored some of the issues surrounding the performance of a whole rocket. What we didn’t explore was the heart of the rocket, the motor. In this section we’ll look at the design of motors, the factors which affect the performance of motors, and some of the practical limitations of motor design. The first part of this section is necessarily descriptive as the chemistry, thermodynamics and maths associated with motor design are beyond the target audience of this website.
General Principles of a Rocket Motor
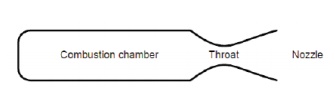
In a rocket motor a chemical reaction is used to generate hot gas in a confined space called the combustion chamber. The chamber has a single exit through a constriction called the throat. The pressure of the hot gas is higher than the surrounding atmosphere, thus the gas flows out through the constriction and is accelerated.
Propellants
The chemical reaction in model rocket motors is referred to as an “exothermal redox” reaction. The term “exothermal” means that the reaction gives off heat, and in the case of rocket motors this heat is mainly absorbed by the propellants raising their temperature.
The term “redox” means that it is an oxidation/reduction reaction, in other words one of the chemicals transfers oxygen atoms to another during the reaction. The two chemicals are called the oxidising agent and the reducing agent.
The most popular rocket motors are black powder motors, where the oxidising agent is saltpetre and the reducing agents are sulphur and carbon. Other motors include Potassium or ammonium perchlorate as the oxidising agent and mixtures of hydrocarbons and fine powdered metals as the reducing agents. Other chemicals are often added such as retardants to slow down the rate of burn, binding agents to hold the fuel together (often these are the hydrocarbons used in the reaction), or chemicals to colour the flame or smoke for effects. In hybrid motors a gaseous oxidiser, nitrous oxide, reacts with a hydrocarbon, such as a plastic, to produce the hot gas.
Energy Conversion
This reaction releases energy in the form of heat, and by confining the gas within the combustion chamber we give it energy due to its pressure. We refer to the energy of this hot pressurised gas as its “enthalpy”. By releasing the gas through the throat the rocket motor turns the enthalpy of the gas into a flow of the gas with kinetic energy. It is this release of energy which powers the rocket. So the energy undergoes Two conversions:
Ø Chemical energy to enthalpy
Ø Enthalpy to kinetic energy
The conversion from chemical energy to enthalpy takes place in the combustion chamber. To obtain the maximum enthalpy it is clearly important to have a reaction which releases lots of heat and generates lots of high energy molecules of gas to maximise pressure here is clearly a limit to the temperature & pressure, as the combustion chamber may melt or split if these are too high. The designer has a limitation placed on his choice of reagents in that the reaction must not heat the combustion chamber to a point where it is damaged, nor must the pressure exceed that which the chamber can survive.
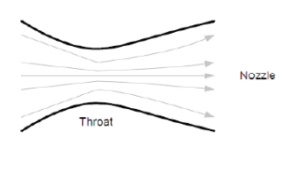
Changing enthalpy to kinetic energy takes place in the throat and the nozzle. Our mass of hot gas flows into the throat, accelerating as the throat converges. If we reduce the chameter of the throat enough, the flow will accelerate to the speed of sound, at which pint something unexpected occurs. As the flow diverges into the nozzle it continues to accelerate beyond the speed of sound, the increase in velocity depending on the increase in area. This type of nozzle is called a De Laval nozzle.
Kinetic energy of a body:
If we consider a small volume of gas, it will have a very low mass. As we accelerate this gas it gains kinetic energy proportional to the square of the velocity, so if we double the velocity we get four times the kinetic energy. The velocity of the supersonic flow increases proportional to the increase in area of the nozzle, thus the kinetic energy increases by the fourth power of the increase in nozzle diameter. Thus doubling the nozzle diameter increases the kinetic energy by 16 times! The De Laval nozzle make rocket motors possible, as only such high velocity flows can generate the energy required to accelerate a rocket.
In model rockets the reaction is chemical generally short lived, a few seconds at most, sothe amount of heat transferred to the structural parts of the motor is limited. Also, the liner of the motor casing acts to insulate the casing from the rapid rise in temperature which would result from a reaction in direct contact with the metal casing. Model rocket motors also run at quite low pressure, well below the limits if the motor casing, further protecting the casing. It can be seen that the enthalpy of a model rocket motor is thus quite low. In large launch vehicles such as Ariane, the pressure and temperature are high, the burn may last several minutes, and the mass budget for the designer is very tight. Designing motors for these purposes is highly complex.
Thrust
The basic principles of a rocket motor are relatively straightforward to understand. In rocketry the motor exists to accelerate the rocket, and thus it has to develop a force called “thrust”. One of several definitions of force is that: Force = rate of change of momentum If we ignore (for a few paragraphs) any external effects we can say that the thrust is entirely due to the momentum of the propellant, a force called the “momentum thrust”. If we denote the thrust as F and the momentum as P, then mathematically:
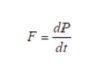
Sometimes for mathematical clarity we us the notation of P with a dot on top to denote the first derivative of P, and with 2 dots for the second derivative. Thus, in this new notation:
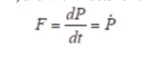
You may also recall from the section on the rocket equation that momentum is the product of the mass and velocity. Thus we can say that the momentum of the flow from the nozzle of the rocket has a momentum:
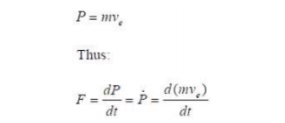
If the exhaust velocity remains constant, which is a reasonable assumption, we arrive at the equation:
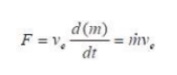
The term “m-dot” is known as the mass flow rate, in other words the rate at which mass is ejected through the nozzle in kg/sec. In other words this is the rate at which the rocket burns fuel. This is an interesting relationship, which can be expressed in words as: Momentum
Thrust = mass flow rate x exhaust velocity
Flow expansion
The propellant is accelerated into the atmosphere.
As it leaves the nozzle the propellant has an exit pressure Pexit and enters an
atmosphere which has a pressure Patm. The transition from one pressure to the
other cannot happen instantaneously as any pressure difference will cause a
flow of high pressure fluid into the low pressure region.
So the force (a component of thrust called “pressure
thrust”) depends on the pressure difference and the area
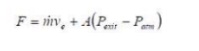
Related Topics