Radiochemical Methods of Analysis: Quantitative Applications

Quantitative Applications

Three common quantitative applications of radiochemical methods of analysis are considered in this section: the direct analysis of radioactive isotopes by measuring their rate of disintegration, neutron activation, and the use of radioactive isotopes as tracers in isotope dilution.

Direct Analysis of Radioactive Analytes 

The concentration of a long-lived ra- dioactive isotope is essentially constant during the period of analysis. As shown in Example 13.6, the sample’s activity can be used to calculate the number of radioac- tive particles that are present.

The direct analysis of short-lived radioactive isotopes using the method out- lined in Example 13.6 is less useful since it provides only a transient measure of the isotope’s concentration. The concentration of the isotope at a particular moment can be determined by measuring its activity after an elapsed time, t, and using equa- tion 13.26 to calculate N₀.

Neutron Activation Analysis 

Few samples of interest are naturally radioactive. For many elements, however, radioactivity may be induced by irradiating the sample with neutrons in a process called neutron activation analysis (NAA). The radioac- tive element formed by neutron activation decays to a stable isotope by emitting gamma rays and, if necessary, other nuclear particles. The rate of gamma-ray emis- sion is proportional to the analyte’s initial concentration in the sample. For exam- ple, when a sample containing nonradioactive  ²⁷₁₃Al is placed in a nuclear reactor and irradiated with neutrons, the following nuclear reaction results.

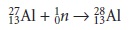
The radioactive isotope of ²⁷₁₃Al has a characteristic decay process that includes the release of a beta particle and a gamma ray.

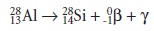
When irradiation is complete, the sample is removed from the nuclear reactor, al- lowed to cool while any short-lived interferences that might be present decay to the background, and the rate of gamma-ray emission is measured.

The initial activity at the end of irradiation depends on the number of ²⁸₁₃Al atoms that are present. This, in turn, is equal to the difference between the rate of formation for ²⁸₁₃Al and its rate of disintegration,

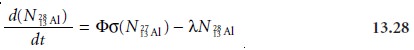
Where Φ  is the neutron flux, and  is the reaction cross-section, or probability for the capture of a neutron by the ²⁷₁₃Al nucleus. Integrating equation 13.28 over the time of irradiation, t_i, and multiplying  by  gives the initial activity, A₀, at the end of irradiation as

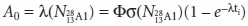
Thus, the number of atoms of  ²⁷₁₃Al initially present in the sample can be calculated from A₀ if values for and Φ,σ,λ,t_i are known.

A simpler approach for analyzing neutron activation data is to use one or more external standards. Letting (A₀)_x and (A₀)_s represent the initial activity for the ana- lyte in an unknown and a single external standard, and letting w_x and w_s represent the weight of analyte in the unknown and the external standard, gives a pair of equations

(A₀)_x = kw_x ……………….13.29

(A₀)_s = kw_s ……………….13.29

that can be solved to determine the mass of analyte in the sample.

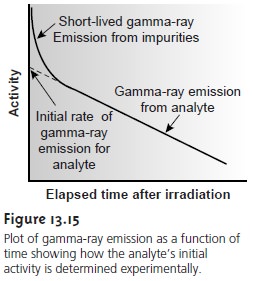
As noted earlier, gamma-ray emission is measured following a “cooling” period in which short-lived interferents are allowed to decay away. The initial activity therefore, is determined by extrapolating a curve of activity versus time back to t = 0 (Figure 13.15). Alternatively, if the samples and standards are irradiated simul- taneously, and the activities are measured at the same time, then these activities may be used in place of (A₀)_x and (A₀)_s in the preceding equations.

One of the important advantages of NAA is its applicability to almost all ele- ments in the periodic table. Another advantage of neutron activation is that it is nondestructive. Consequently, NAA is an important technique for analyzing ar- chaeological and forensic samples, as well as works of art.

Isotope Dilution 

Another important quantitative radiochemical method is isotope dilution. In this method of analysis a sample of analyte, called a tracer, is prepared in a radioactive form with a known activity, A_T, for its radioactive decay. A mea- sured mass of the tracer, w_T, is added to a sample containing an unknown mass, w_x, of a nonradioactive analyte, and the material is homogenized. The sample is then processed to isolate w_A grams of purified analyte, containing both radioactive and nonradioactive materials. The activity of the isolated sample, A_A, is measured. If all the analyte, both radioactive and nonradioactive, is recovered, then A_A and A_T will be equal. Normally, some of the analyte is lost during isolation and purification. In this case A_A is less than A_T, and

The ratio of weights in equation 13.31 accounts for the “dilution” of the activity due to a failure to recover all the analyte. Solving equation 13.31 for w_x gives

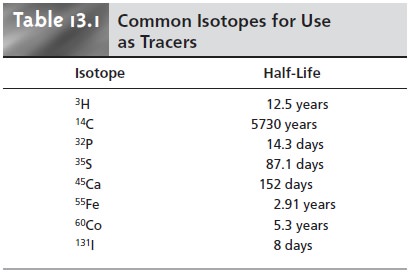
Equations 13.31 and 13.32 are only valid if the radioactive element in the tracer has a half-life that is considerably longer than the time needed to conduct the analysis. If this is not the case, then the decrease in activity is due both to the effect of dilu- tion and the natural decrease in the isotope’s activity. Some common radioactive isotopes for use in isotope dilution are listed in Table 13.1.

An important feature of isotope dilution is that it is not necessary to recover all the analyte to determine the amount of analyte present in the original sample. Iso- tope dilution, therefore, is useful for the analysis of samples with complex matrices, when a complete recovery of the analyte is difficult.