Q-Meter

Q-Meter

Every inductor coil has a certain amount of resistance and the coil should have lowest possible resistance. The ratio of the inductive reactance to the effective resistance of the coil is called the quality factor or Q-factor of the coil. So Q = X_L/ R = ωL / R

A high value of Q is always desirable as it means high inductive reactance and low resistance. A low value of Q indicates that the resistance component is relatively high and so there is a comparatively large loss of power.

The effective resistance of the coil differs from its dc resistance because of eddy current and skin effects and varies in a highly complex manner with the frequency. For this reason Q is rarely computed by determination of R and L

One possible way for determination of Q is by using the inductance bridge but such bridge circuits are rarely capable of giving accurate measurements, when Q is high. So special meters are used for determination of Q accurately.

The Q-meter is an instrument designed for the measurement of Q-factor of the coil as well as for the measurement of electrical properties of coils and capacitors. -This instrument operates on the principle of series resonance i.e. at resonate condition of an ac series circuit voltage across the capacitor is equal to the applied voltage times of Q of the circuit. If the voltage applied across the circuit is kept-constant then voltmeter connected across the capacitor can be calibrated to indicate Q directly.

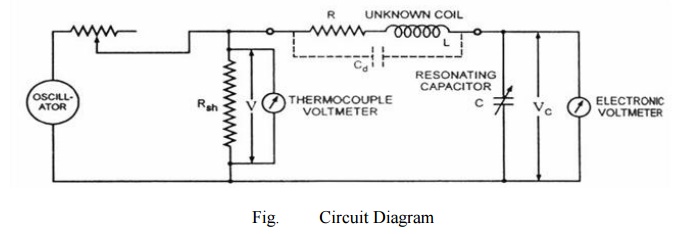
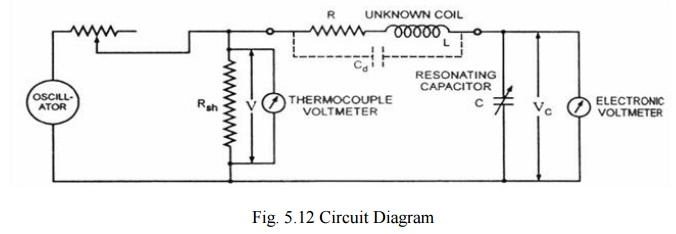
Circuit diagram of a Q-meter is shown is figure. A wide-range oscillator with frequency range from 50 kHz to 50 MHz is used as a power supply to the circuit. The output of the oscillator is shorted by a low-value resistance, R_sh usually of the order of 0.02 ohm. So it introduces almost no resistance into the oscillatory circuit and represents a voltage source with a very small or of almost negligible internal resistance. The voltage across the low-value shunt resistance R_sh, V is measured by a thermo-couple meter and the voltage across the capacitor, V_c is measured by an electronic voltmeter.

For carrying out the measurement, the unknown coil is connected to the test terminals of the instrument, and the circuit is tuned to resonance either by varying the frequency of the oscillator or by varying the resonating capacitor C. Readings of voltages across capacitor C and shunt resistance R_sh are obtained and Q-factor of the coil is determined as follows :

By definition Q-factor of the coil, Q = X_L/ R

And when the circuit is under resonance condition X_L= X_COr IX_L= IX_C= V_C

And the voltage applied to the circuit. V = IR So, Q = X_L/ R = IX_L/ R = V_C/ V This Q-factor is called the circuit Q because this measurement includes the losses of the resonating capacitor, voltmeter and the shunt resistor R_sh. So, the actual Q-factor of the coil will be somewhat greater

than the calculated Q-factor. This difference is usually very small and maybe neglected except when the resistance of the coil under test is relatively small in comparison to the shunt resistance R_sh. The inductance of the coil can also be computed from the known values of frequency f and resonating capacitor C as follows. At resonance, X_L= X_Cor 2Ï€fL = 1/2Ï€fC or L = 1/ (2Ï€f)² Henry.