Chapter: 11th 12th std standard Indian Economy Economic status Higher secondary school College
Producer's Equilibrium and The Cobb Douglas Production Function
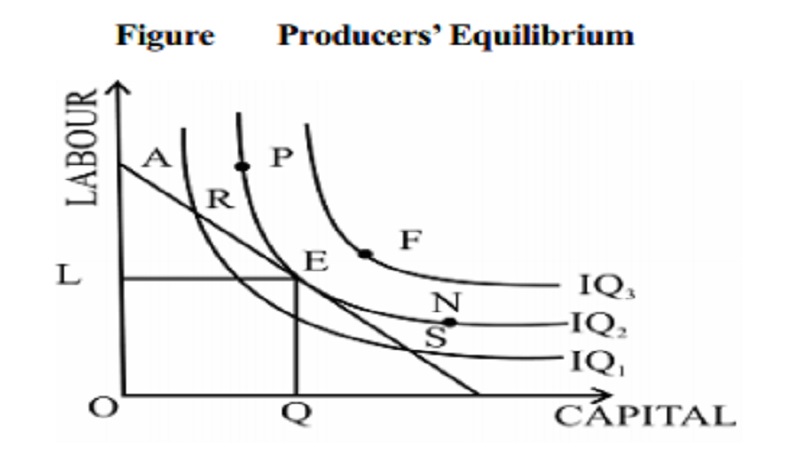
Producer's Equilibrium
A rational producer always tries to achieve largest volume of output from a given factor-expenditure outlay on factors such that these factors are combined in an optimal or most efficient way. The producer maximises his profits and produces a given level of output with least combination of factors. This level of cost combination of factors will be optimum for him In figure, E is the point of equilibrium, where isoquant IQ2 is tangential to isocost line at AB. Given budget line AB, points 'P', 'N' and 'F' are beyond the reach of the producer and points 'R' and 'S' on isoquant IQ1 give less output than the output at the point of equilibrium 'E' which is on IQ2. The amount spent on combinations R, E, S is the same as all the three points lie on the same isocost line. But the output produced at point E is higher as E lies on a higher isoquant. Given the isocost line and the series of isoquants (isoquant-map), a producer will choose that level of output, where a given isocost line is tangential to the highest possible isoquant.

Thus the producer is in equilibrium at point E where the isoquant is tangential to the isocost line. At this point, the slopes of the isoquant and the isocost line are equal. Thus at the equilibrium point the marginal rate of technical substitution is equal to the price ratio of factors. Hence, the condition for producers' equilibrium is
MRTSxy = PX/PY
At this point of equilibrium, the combination E (that is OL of labour and OQ of capital) is called least cost
The Cobb - Douglas Production Function
The simplest and the most widely used production function in economics is the Cobb-Douglas production function. It is a statistical production function given by professors C.W. Cobb and P.H. Douglas.
The Cobb-Douglas production function can be stated as follows
Q = bL a C 1 − a in which
Q = Actual output
L = Labour
C = Capital
b = number of units of Labour
a = Exponent∗ of labour
1-a = Exponent∗ of Capital
According to the above production function, if both factors of production (labour and capital) are increased by one percent, the output (total product) will increase by the sum of the exponents of labour and capital i.e. by (a+1-a). Since a+1-a =1, according to the equation, when the inputs are increased by one percent, the output also increases by one percent. Thus the Cobb Douglas production function explains only constant returns to scale. This is mainly because the addition of Q bLa C b
In the above production function, the sum of the exponents shows the degree of 'returns to scale' in production function.
a + b >1 : Increasing returns to scale
a + b =1 : Constant returns to scale
a + b <1 : Decreasing returns to scale
Large Scale Production - Kinds of Economies
Related Topics