Chapter: Civil : Mechanics Of Solids : Thin Cylinders, Spheres And Thick Cylinders

Principal planes and stresses

The normal stresses ( x' and y') and the shear stress ( x'y') vary smoothly with respect to the rotation an accordance with the coordinate transformation equations.

Principal planes and stresses

Principal stresses and planes

Principal Directions, Principal Stress

The normal stresses ( x' and y') and the shear stress ( x'y') vary smoothly with respect to the rotation an accordance with the coordinate transformation equations. There exist a couple of particular angles where the take on special values.

First, there exists an angle p where the shear stress x'y' becomes zero. That angle is found by setting x'y' t the above shear transformation equation and solving for (set equal to p). The result is,

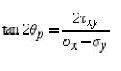
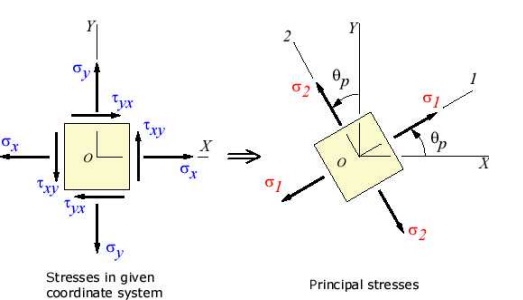
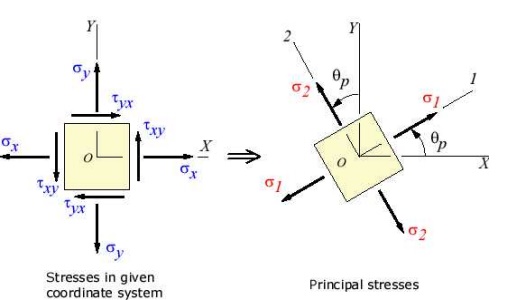
The angle _p defines the principal directions where the only stresses are normal stresses. These stre called principal stresses and are found from the original stresses (expressed in the x,y,z directions) via,

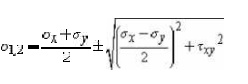
The transformation to the principal directions can be illustrated as:

Maximum Shear Stress Direction

Another important angle, _s, is where the maximum shear stress occurs. This is found by finding the maximu shear stress transformation equation, and solving for . The result is,

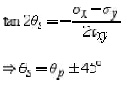
The maximum shear stress is equal to one-half the difference between the two principal stresses,

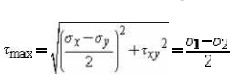
The transformation to the maximum shear stress direction can be illustrated as:

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

Civil : Mechanics Of Solids : Thin Cylinders, Spheres And Thick Cylinders : Principal planes and stresses |