Prestressed Concrete Structures: Losses

Losses

Elastic Shortening (ES) - Cl 18.5.2.4

Shortening in steel that occurs as soon as Fi is transferred to the concrete member and the member as a whole shortens.

Fi = Pre-stress just before transfer

F = Final stress after losses

Fo = Immediately after transfer - very difficult to estimate

Note: The value of Fo may not be known, but it is not necessary, as the losses from Fi to Fo small percentage of Fi . Total accuracy is relative anyway, as Ec - the young's modulus of concrete cannot be determined accurately.

Creep (CR) Cl 18.5.2.1

Among the many factors affecting creep are volume to surface ratio, age of concrete at time of pre- stress, relative humidity, type of concrete (lightweight / normal). Creep is assumed to occur in the member after permanent loads are imposed after pre-stress. Creep occurs over a long period of time under sustained load. Part of initial compressive strain induced in concrete immediately after transfer is reduced by the tensile strain produced by superimposed permanent loads.

Therefore for bonded members, loss due to creep

f_cds = stress in concrete at steel level due to superimposed dead loads applied to the member after transfer of pre-stress

Shrinkage of concrete (SH) Cl 18.5.2.2

Factors like volume to surface ratio, relative humidity, time from end of moist curing to application of pre-stress, affect shrinkage in concrete. Shrinkage is time-dependant and about 80% of the final loss due to shrinkage occurs in the first year and 100% after several years.

Shrinkage strain

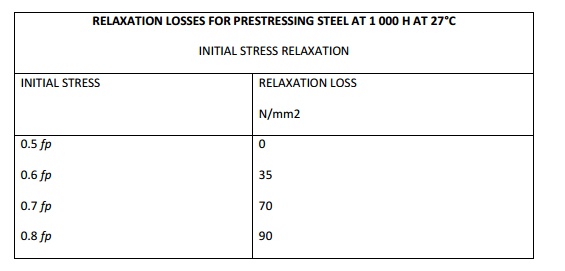
Relaxation of steel (RE) Cl 18.5.2.3

When elongation is sustained over pre-stressing cable for a long time, the pre-stress will decrease gradually. The RE - loss due to relaxation depends on type of steel, time, as well as the ratio of f_i/f_p i where fi is the initial pre-stress and f_p is the characteristic strength of steel.

Anchorage slip (ANC) Cl 18.5.2.5

In post-tensioning, when the jack is released, the full pre-stress is transferred to the anchorage and they tend to deform, allowing the tendon to slacken. Friction wedges will slip a little before they grip the wire firmly. So, in post-tensioning the wedges are positively engaged before the jack is released. In pre- tensioning also, the anchorage slip is compensated for during stressing operation.

The loss is caused by a fixed shortening of the anchorages, so the percentage loss is higher in shorter wires than in long ones.

Frictional loss Cl 18.5.2.6

Frictional loss comprise of two parts: (1) The length effect and (2) The curvature effect. The length effect or the wobble effect of the duct is the friction that will exist between straight tendon and the surrounding material. This loss is dependant on the length and stress in the tendon, the coefficient of friction between the contact materials, the workmanship and the method used in aligning and obtaining the duct.

The curvature effect is the loss due to intended curvature of the tendon. This again depends on the coefficient of friction between the materials and the pressure exerted by the tendon on the curvature.

For un-bonded tendon, lubrication, in the form of grease and plastic tube wrapping can be used to advantage.

For bonded tendon lubricant in the form of water soluble oils are used during stressing operation and flushed off with after before grouting.

Jacking from both ends of the beam will also reduce loss due to friction.

For straight or moderately curved structures, with curved or straight cables, the value of pre-stressing force Px at a distance x meters from tensioning end and acting in the direction of the tangent to the curve of the cable, shall be calculated as below:

P_x = P_oe ^{- ( ?? + kx ).}

Where Po = pre-stressing force in the pre-stressed steel at the tensioning end acting in the direction of the tangent to the curve of the cable, ? = cumulative angle in radians through which the tangent to the cable profile has turned between any two points under consideration, ? = coefficient of friction in curve; unless otherwise proved by tests, ? may be taken as: 0.55 for steel moving on smooth concrete, 0.30 for steel moving on steel fixed to duct, and 0.25 for steel moving on lead, k = coefficient for wobble or wave effect varying from 15 × 10-4 to 50 × 10-4 per meter. The expansion of the equation for Px for small values of (?? + kx) may be P_x = P_o (1 - ?? - kx).

Examples

To calculate ES in Pre-tensioned beam - eccentric tendon

A pre-tensioned beam of 100 mm x 300 mm is pre-stressed by straight wires with F_i = 150 kN at an e = 50 mm. E_S = 2.1x10 MPa, E_C = 0.35x10⁵ MP_a and AP = 188 mm Estimate ES

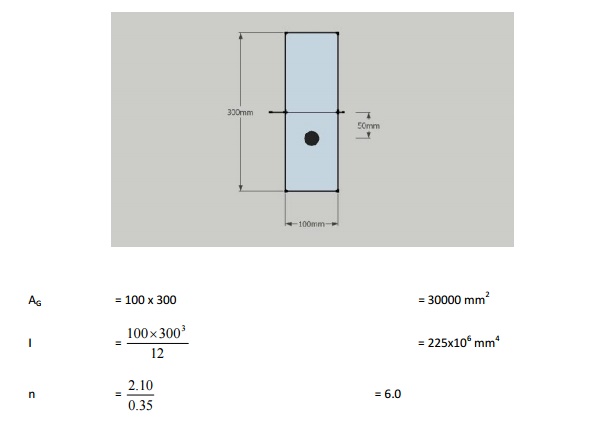
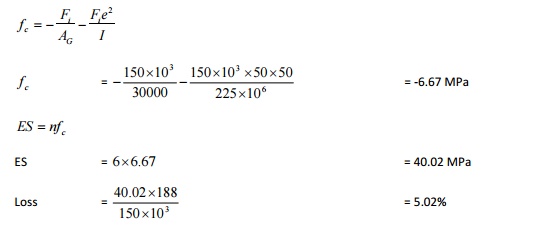
ES in Pre-tensioned beam - concentric tendon

A straight pre-tensioned beam 12 m long of 380 mm x 380 mm is concentrically pre-stressed with 780 mm 2 wires anchored to bulkheads with a f_i = 1035 MPa. E_s = 2x10⁵ MPa, E_c=0.33x10⁵ Mpa

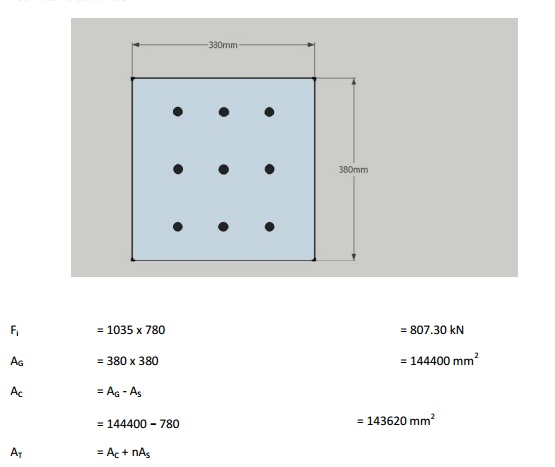
ES in Pre-tensioned beam - Eccentric tendons at top & bot

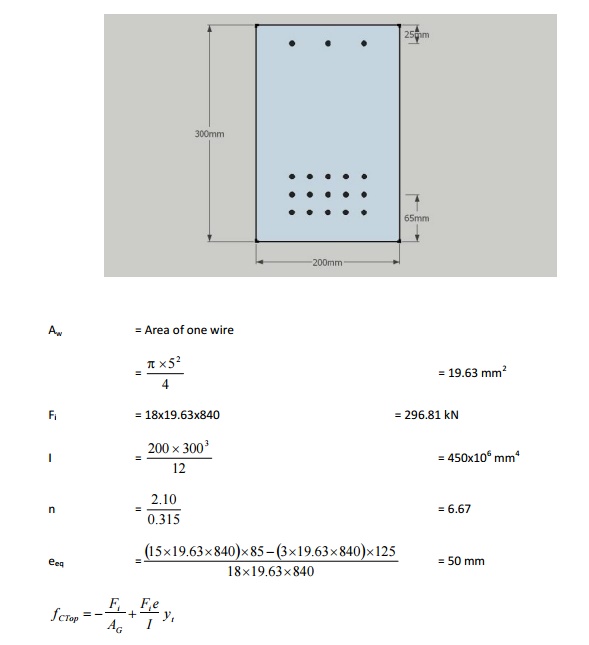
A pre-tensioned beam of 200 mm x 300 mm is pre-stressed with 15#5mm  f  wires located at 65 mm  from the bottom of the beam and 3#5mm ? wires located at 25mm from the top of the beam. f _i = 840MPa.E_S =2.x10MPa,E_C =0.315x10⁵ MPa Estimate ES. transfer.

To calculate ES in Post-tensioned beam

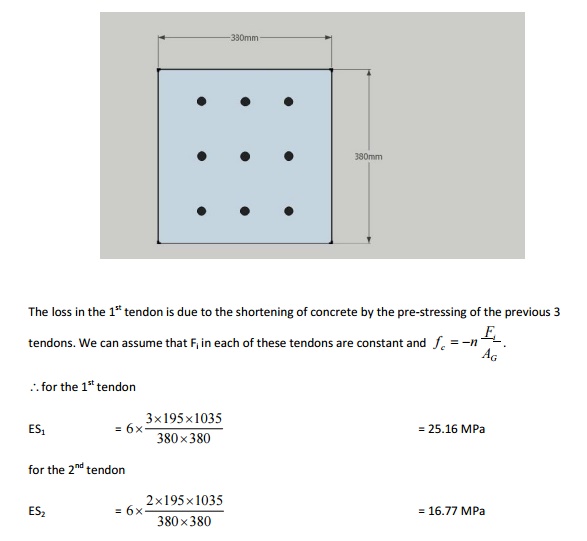
A straight post-tensioned beam 12 m long of 380 mm x 380 mm is concentrically pre-stressed with 780 mm² wires made up of 4 tendons with 195 mm²  and the tendons are pre-stressed sequentially with a f = 1035 MPa. ES = 2x10 MPa, EC = 0.33x10⁵ MPa. Estimate ES at transfer.

To calculate CR, SH and RE in post-tensioned beam

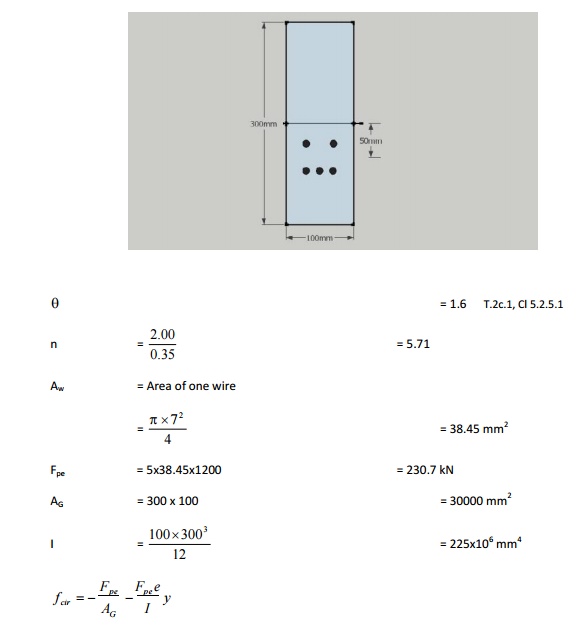
A straight post-tensioned beam of size 100 mm x 300 mm is pre-stressed with 5 wires of 7 mm f. The 5 average pre-stress after short-term losses is f _pe= 1200 MPa. The gae at loading is 28 days. E_S = 2x10⁵  MPa, EC = 0.35x10⁵ MPa. Estimate CR, SH and RE assuming fp = 1715 MPa.

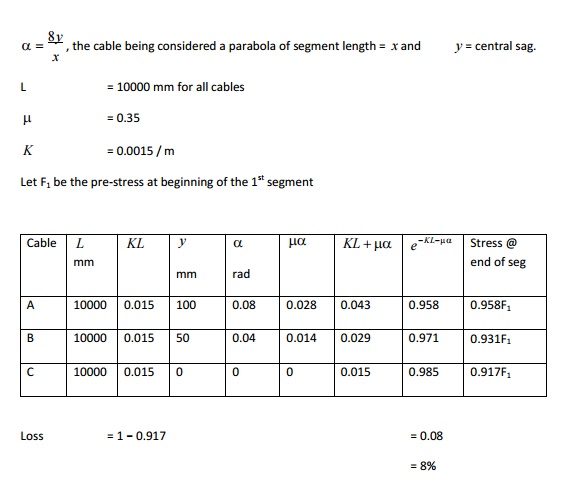
To calculate frictional losses - tensioned from one end

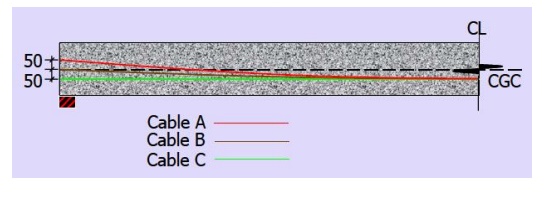
A post-tensioned beam 100 mm × 300 mm of le = 10 m is stressed by successive tensioning and anchoring of 3 cables A, B, and C respectively as shown in figure. Each cable has cross section area of 200 mm² and has initial stress of 1200 MPa. If the cables are tensioned from one end, estimate the percentage loss in each cable due to friction at the anchored end. Assume ? = 0.35, K = 0.0015 / m.

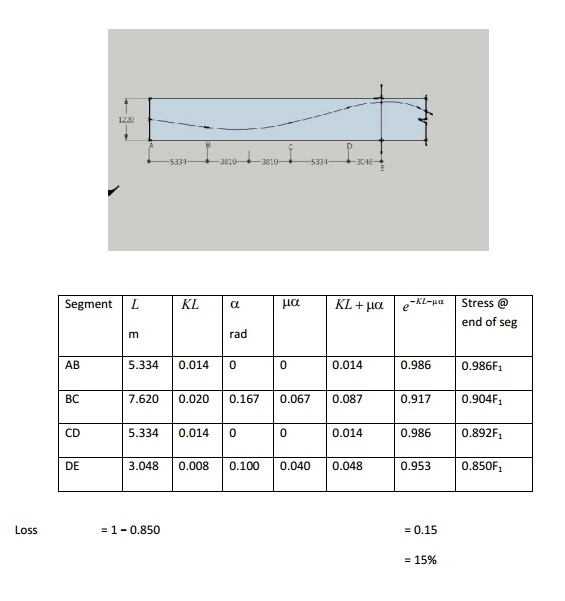
To calculate frictional losses - tensioned from both ends

A pre-stressed concrete beam is continuous over two spans and its curved tendon is to be tensioned from both ends. Compute the percentage of loss of pre-stress due to friction from one end to the center of the beam (A-E). The coefficient of friction between the cable and the duct is 0.40 and the average wobble or length effect is represented by k = 0.0026/m. The cable is straight between A-B and C-D. The change in angle between BC is 0.167 radians and that between DE is 0.100 radians.