Potentiometric Methods: Theory

THEORY

In a situation, where a metal M is placed in a solution containing its own ions Mⁿ⁺, an electrode potential is established across the two electrodes, whose actual value is provided by the Nernst equation as shown below :

E = E^– + (RT/nF) ¹n a Mⁿ⁺                   ..(b)

From Eq. (b) the relationship to a cationic electrode, i.e., sensitive only to a cation concentration, may be expressed as :

E = E^– Yⁿ⁺, Y + (RT/nF) ¹n aYⁿ⁺.........................(c)

to an anionic electrode :

E = E^– X^n–, X – (RT/nF) ¹n a X^n–.........................(d)

or to a redox electrode :

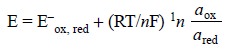       ..........................(e)

where,  

E– = Standard electrode potential (SEP)    (or reduction potential of the half-cell involved),      

a = Thermodynamic activity of the ion to which the electrode is sensitive,         

R = Gas constant (8.314 JK^–1 mol^–1),        

T = Absolute temperature (K),         

F = Faraday (96500 C/mole of electrons), and    

n = Number of electrons involved in the electrode reaction.   

Direct Potentiometry : The procedure adopted of employing a single measurement of electrode potential to determine the concentration of an ionic species in a solution is usually termed as direct potentiometry.

Disadvantages : Direct potentiometry has the following two serious disadvantages namely :

(a) From the Nernst Eq. (b) : Considering n = 1, temperature 25°C, RT/nF being a constant, and introducing the factor for the conversion of natural logarithms to logarithms to base 10, the term RT/nF shows a value of 0.0591 V. Therefore, for an ion M⁺ (monovalent) a ten-time change in the electrode potential E by approximately 60 millivolts (mV) ; whereas for an ion M²⁺ (bivalent) a change in identical magnitude of activity shall bring forth alternation of E by about 30 mV. Hence, it is evident that to attain a desired accuracy and precision to the extent of 1% in the estimated value for the direct concentration using the technique of direct potentiometry, for M⁺ ion—the E should be measurable correctly within 0.26 mV ; and for M²⁺ ion-within 0.1 mV.

(b) Uncertainty due to liquid-junction potential (E_j) : It has been observed that the liquid-junction potential (E_j) occurring between the two solutions, one related to the reference-electrode and the other to the indicator-electrode gives rise to a certain quantum of uncertainty with regard to e.m.f. measurement.

Remedial Measures : There are two ways to eliminate the above anomaly, namely :

(i)          to replace the reference electrode with a concentration-cell i.e., with an electrode comprised of a rod of the same metal as that employed in the indicator electrode plus a solution having the same cation as present in the test-solution, but with a known concentration. Thus, the ionic activity of the metal ion present in the test-solution may be represented by the following expression :

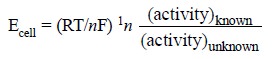            ....................(f)

(ii) by using one solution which contains a high concentration of KCl or NH₄NO₃ i.e., such electro-lytes that offer almost identical values for ionic conductivities for both cation as well as anion.

Keeping in view the above serious anomalies commonly encountered with direct potentiometry, such as : an element of uncertainty triggered by liquid junction potential (E_j) and high degree of sensitivity required to measure electrode potential (E), it promptly gave birth to the phenomenon of potentiometric titrations,

which subsequently received a high level of sophistication and ultimately turned into a versatile analytical method. As the name suggests, it is indeed a titrimetric method whereby a series of potentiometric measurements are recorded so as to locate the end-point as correctly as possible. In this procedure, it is particularly of more interest to know the exact changes in the observed electrode potential after each addition of the titrant, rather than a precise and accurate electrode potential often brought about by a given solution. Thus, in a way the impact due to liquid-junction-potential (E_j) has been eliminated completely. It is pertinent to mention here that in a potentiometric titration procedure the apparent change in cell e.m.f. takes place not only most rapidly but also most distinctly in the vicinity of the end-point.

1. GENERAL CONSIDERATIONS

The potentiometric titrations invariably cover a broad-spectrum of chemical reactions that may be classified as follows :

(i) Neutralization reactions,

(ii) Redox reactions,

(iii) Precipitation reactions,

(iv) Complexation reactions, and

(v) Potentiometric titrations in non-aqueous solvents.

The general principles which govern the above different types of reactions will be discussed briefly in the sections that follow :

1.1. Neutralization Reactions

The accuracy and precision with which the end-point can be determined potentiometrically solely depends upon the quantum of change in the observed e.m.f. in the vicinity of the equivalence point, which in turn entirely depends upon the strength and the concentration of acid and base employed.

Merits of the Method : It is found to be useful to titrate a mixture of acids having a significant difference in their strengths, for instance : HCl and CH₃COOH (alcoholic). In this case, the first-break in the titration curve signifies that the stronger of the two acids i.e., HCl, gets neutralized ; whereas, the second-break represents the entire completion (i.e., HCl + CH₃COOH).

In order to get fruitful and reproducible results it is quite necessary that the strengths between either the two acids or bases in question must vary by at least 10⁵ to 1.

Demerits of the Method : The neutralization reactions often found to be giving unsatisfactory results in the following two instances. They are :

(a) when both the acid and the base are appreciably weak, and

(b) when either the acid or the base is very weak (i.e., K < 10^–8) and also the prevailing solutions are dilute.

Note : In (a) above, an accuracy upto 1% is achievable in 0.1 M solution.

Choice of Electrodes :

Indicator Electrodes : Hydrogen, Glass or Antimony electrodes ;

Reference Electrode : Calomel electrode.

1.2. Redox Reactions

In this particular case the ratio of the concentrations of the oxidized and reduced forms of ionic species establishes the determining factor. Considering the following reaction,

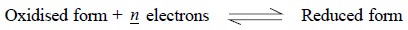
The electrode potential E is given by the following expression :

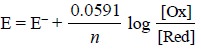               .....................(g)

where,  E^– = Standard potential of the system.

In other words, the potential of the immersed indicator electrode is solely controlled and monitored by the ratio of the ionic concentrations in Eq. (g). Furthermore, in the course of either reduction of an oxidizing agent or vice-versa i.e. the said ratio, and hence the observed potential, undergoes an instant rapid change in the proximity of the end-point of the redox reaction.

Example : A typical example is that of titrations of Fe²⁺ with potassium permanganate or potassium dichromate or cerium (IV) sulphate.

Choice of Electrode : Indicator Electrode : Pt wire or foil.

The oxidizing agent is usually taken in the burette.

1.3. Precipitation Reactions

In this the determining factor mainly rests on the solubility product of the resulting nearly insoluble material generated in the course of a precipitation reaction and its ionic concentration at the equivalence point. It is, however, pertinent to mention here that the indicator electrode must readily come into equilib-rium with one of the ions.

Example : Titration of Ag⁺ with a halide (Cl^–, Br^– or I^–) or with SCN^– (thiocyanate ion).

Choice of Electrodes :

Reference Electrodes :  Saturated Calomel Electrode (SCE) :

Silver-silver chloride Electrode ;

Indicator Electrodes :      Silver wire or Platinum wire or gauze plated with silver and sealed into a glass-tube.

(It should readily come into equilibrium with one of the ions of the precipitate).

Salt-Bridge :                     For the determination of a halide the salt-bridge should be a saturated solution of potassium nitrate.

Note : Ion-selective electrode can also be employed.

1.4. Complexation Reaction

Complexation invariably occurs by the interaction of a sparingly soluble precipitate with an excess amount of the reagent, for instance : the classical example of titration between KCN and AgNO₃ as expressed by the following reactions :

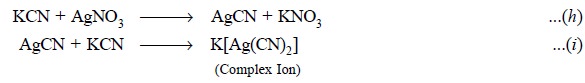
In Eq. (h) the precipitate of AgCN is produced at first instance ; consequently, the precipitate of AgCN initially produced gets dissolved by further addition of KCN to afford the complex ion [Ag(CN)₂]^– Eq. (i) and only a negligible quantum of Ag⁺ ions remain in the solution. Thus, the entire process from ab initio to the final stage of titration may be divided into three distinct portions, namely :

(i) Upto end-point : Here, all the available CN^– ion has been virtually converted to the complex ion. At this stage the ever increasing concentration reflects a gradually increasing concentration of Ag⁺ ions, thereby slowly enhancing the potential of the Ag-electrode dipping in the solution,

(ii) At the end-point : It is usually visualized by a distinct and marked rise in potential, and (iii) Beyond end-point : Further addition of AgNO₃ brings about only a gradual change in e.m.f. and AgCN gets precipitated. Ultimately, a second sudden change in potential may be visualized at this juncture when practically most of the CN^– ion gets precipitated as AgCN.

Choice of Electrodes :

Indicator Electrode : Silver electrode ;

Reference Electrodes : Colomel electrode ; Mercury-mercury (I) sulphate electrode.

Salt-Bridge : A saturated solution of KNO₃ or K₂SO₄ isolated from the reference electrode.

1.5. Potentiometric Titration in Non-Aqueous Solvents

The potentiometric technique has proved to be of great significance and utility for determining end-points of titrations in a non-aqueous media. The mV scale rather than the pH scale of the potentiometer must be used for obvious reasons, namely :

(i) pH scale based upon buffers has no logical significance in a non-aqueous media, and

(ii) the potentials in non-aqueous media may exceed the pH scale.

The resulting titration curves are more or less emperical and afford a reasonably dependable and reproducible means of end-point detection.

Choice of Electrodes :

Indicator Electrodes : Glass electrode ;

Reference Electrode: Calomel electrode ;

Salt-Bridge: A saturated solution of KCl.

2. END-POINT DETERMINATION

In fact, there are several acceptable means to graph the potentiometric titration data generated from an actual titration in order to locate the exact (or nearest) end-point. These may be illustrated exclusively by employing the titration data provided in Table 16.1, between 25 ml of 0.01 M NaF and 0.01 M La (NO₃)₃.

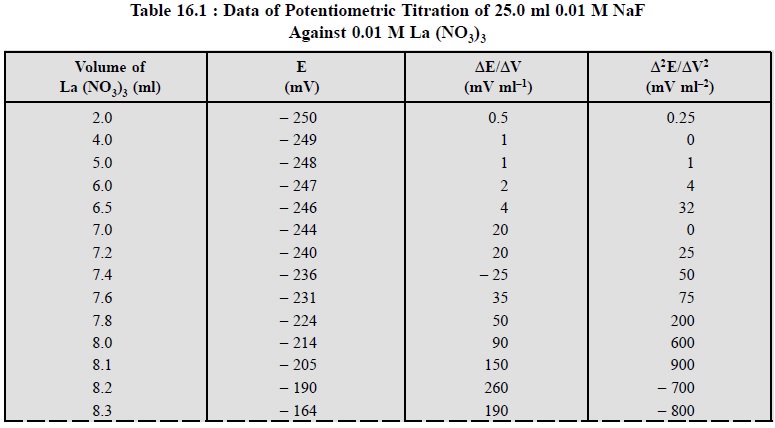
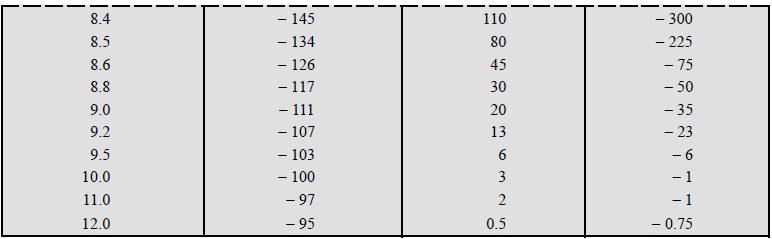
The simplest and the most commonly used method is to plot the cell voltage E, millivolts (mV), versus the volume (ml) of titrant added. Ultimately, the end-point is determined from the point of maximum slope of the curve i.e., the point of inflexion, as depicted in Figure 16.1 (a). However, the degree of accuracy and precision with which this point of inflexion can be located from the plotted graph largely depends on the individual number of data points observed in the close proximities of the end-point.

Figure 16.1 (a) gives rise to a sigmoid-curve (or S-shaped curve) obtained either by using an appropriate equipment (automatic titrators) that plots the graph automatically* as the titration proceeds, or manually by plotting the raw experimental data. The central portion of the sigmoid curve, in fact is the critical zone where the point of inflexion resides and this may be located by adopting any one of the follow-ing three procedures, namely :

(i)          Method of parallel tangents,

(ii)       Method of bisection, and

(iii)     Method of circle fitting

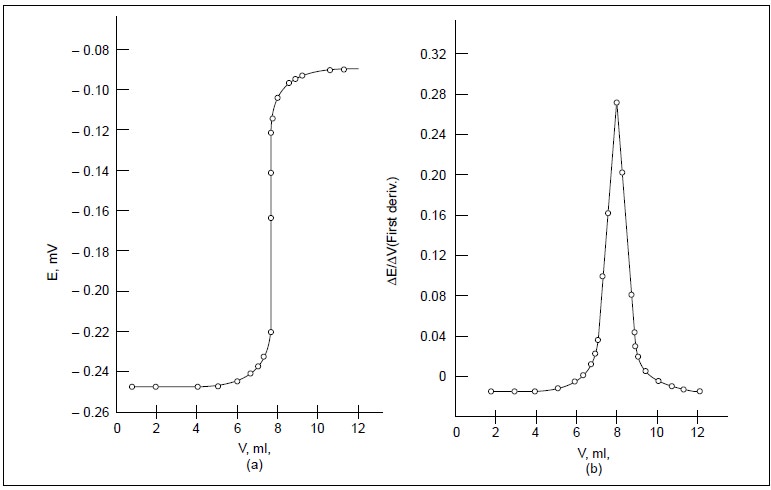
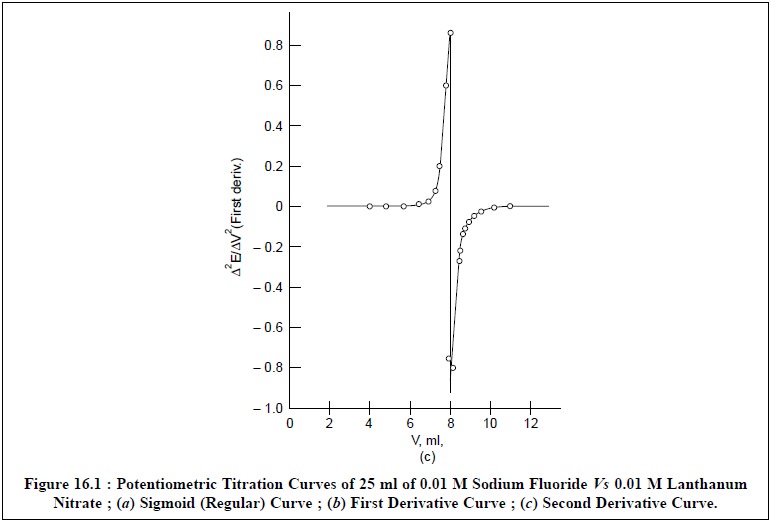
Figure 16.1 (b) is obtained by plotting ∆E/∆V against V which is termed as the first derivative curve. It gives a maximum at the point of inflexion of the titration curve i.e., at the end-point.

Figure 16.1 (c) is achieved by plotting the slope of the frst derivative curve against the volume of titrant added i.e., by plotting ∆²E/∆V² Vs V and is known as the second derivative curve. Thus, the second derivative becomes zero at the point of inflexion and hence, affords a more exact measurement of the equiva-lence point.

The titration error (i.e., difference between end-point and equivalence point) is found to be small when the potential change at the equivalence point is large. Invariably, in most of the reactions employed in potentiometric analysis, the titration error is normally quite small and hence may be neglected.