Pascal’s Triangle

Pascal’s Triangle

The triangle of numbers created by the famous French Mathematician and philosopher Blaise Pascal which is named after him as Pascal’s Triangle. This Pascal’s Triangle of numbers provides lot of scope to observe various types of number patterns in it.

Activity

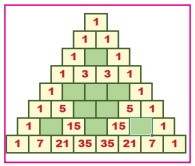
1. Complete the following Pascal’s Triangle by observing the number pattern.

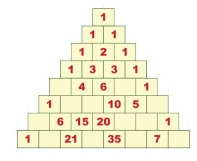
Solution:

2. Observe the above completed Pascal’s Triangle and moving the slanting strips, find the sequence that you see in it and complete them. One is done for you

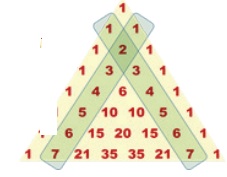
(i) 1, 2, 3, 4, 5, 6, 7.

(ii) 1, 3, 6, 10, 15, 21.

(iii) 1, 4, 10, 20, 35.

(iv) 1, 5, 15, 35.

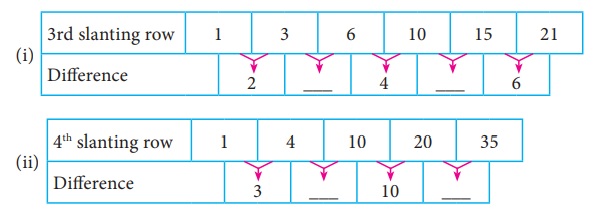
 3. Observe the sequence of numbers obtained in the 3rd and 4th slanting rows of Pascal’s Triangle and find the difference between the consecutive numbers and complete the table given below.

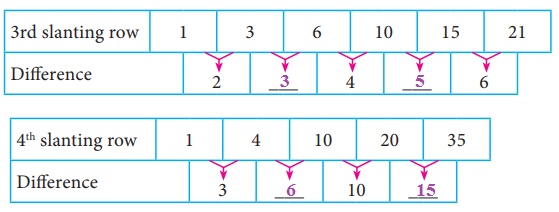
Solution:

Example 5.2

Tabulate the 3rd slanting row of the Pascal’s Triangle by taking the position of the numbers in the slanting row as x and the corresponding values as y.

Verify whether the relationship, y = [ x(x+1) ] /2 between x and y for the given values is true.

Solution

Observe the table carefully. To verify the relationship between x and y, let us substitute the values of x and get the values of y.

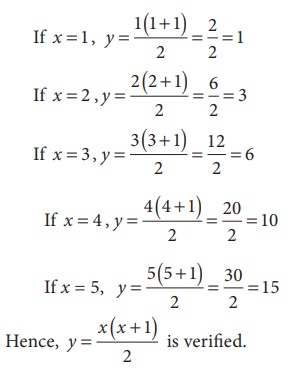
Think

The values of y are obtained by half of the product of the two consecutive values of x.

Example 5.3

 Can row sum of elements in a Pascal’s Triangle form a pattern?

Solution

The row sum of elements of a Pascal’s Triangle are shown below:

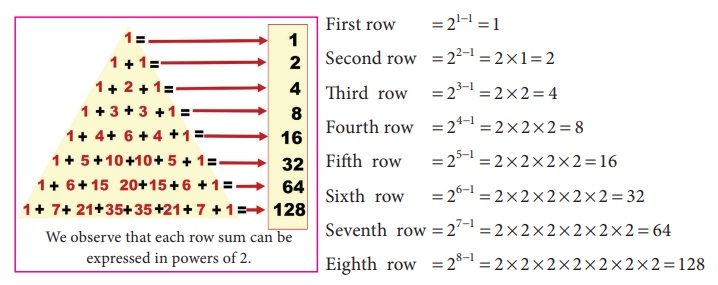
First row = 2^1−1 =1

Second row = 2^2-1=2 × 1=2

Third row =2^3-1=2 × 2=4

Fourth row ==2^4-1=2 × 2 × 2=8

Fifth row = 2^5-1=2 × 2 × 2 × 2=16

Sixth row = 2^6-1=2 × 2 × 2 × 2 × 2=32

Seventh row = 2^7-1=2 × 2 × 2 × 2 × 2 × 2=64

Eighth row = 2^8-1=2 × 2 × 2 × 2 × 2 × 2 × 2=128

Here x denotes the row and y denotes the corresponding row sum. The values of x and y can be tabulated as follows:

The relationship between x and y is y = 2^x–1_.

DO YOU KNOW

Observe the pattern obtained by adding the elements in the slanting rows of the Pascal’s Triangle.

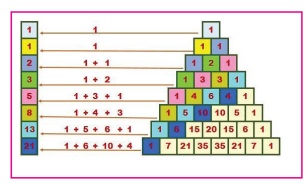
The sequence obtained is known as Fibonacci sequence.

Try these

1. Observe the pattern of numbers given in the slanting rows earlier and complete the Pascal’s Triangle.

Solution :

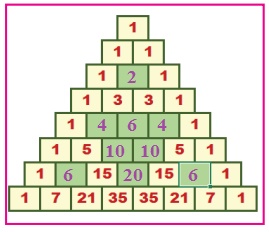
2. Complete the given Pascal’s Triangle. Find the common property of the numbers filled by you. Can you relate this pattern with the pattern discussed in situation 2. Discuss.

Solution :

Example 5.4

Observe the numbers in the hexagonal shape given in the Pascal’s Triangle. The product of the alternate three numbers in the hexagon is equal to the product of remaining three numbers. Verify this

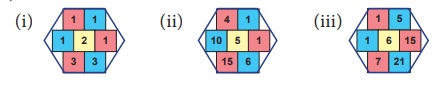
Solution

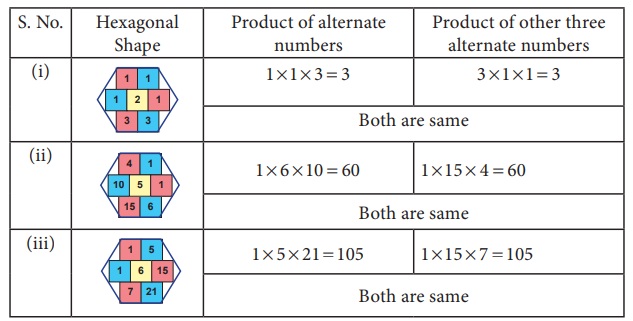
Think

The numbers 1, 3, 6, 10, ... form triangles and are known as triangular numbers. How?