Newton’s Laws of Motion

NEWTON’S LAWS OF MOTION

1. Newton’s First Law

This law states that every body continues to be in its state of rest or the state of uniform motion along a straight line unless it is acted upon by some external force. It gives the definition of force as well as inertia.

2. Force

Force is an external effort in the form of push or pull, which:

1. produces or tries to produce the motion of a static body.

2. stops or tries to stop a moving body.

3. changes or tries to change the direction of motion of a moving body.

Force has both magnitude and direction.

So, it is a vector quantity.

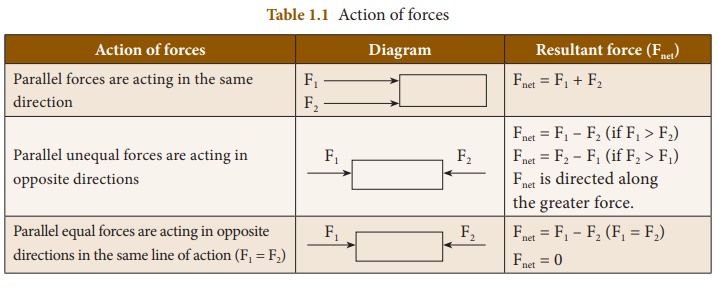
3. Types of forces

Based on the direction in which the forces act, they can be classified into two types as:

(a) Like parallel forces and (b) Unlike parallel forces.

a) Like parallel forces: Two or more forces of equal or unequal magnitude acting along the same direction, parallel to each other are called like parallel forces.

b) Unlike parallel forces: If two or more equal forces or unequal forces act along opposite directions parallel to each other, then they are called unlike parallel forces. Action of forces are given in Table 1.1.

4. Resultant Force

When several forces act simultaneously on the same body, then the combined effect of the multiple forces can be represented by a single force, which is termed as ‘resultant force’. It is equal to the vector sum (adding the magnitude of the forces with their direction) of all the forces.

If the resultant force of all the forces acting on a body is equal to zero, then the body will be in equilibrium. Such forces are called balanced forces. If the resultant force is not equal to zero, then it causes the motion of the body due to unbalanced forces

Examples: Drawing water from a well, force applied with a crow bar, forces on a weight balance, etc.

A system can be brought to equilibrium by applying another force, which is equal to the resultant force in magnitude, but opposite in direction. Such force is called as ‘Equilibrant’.

5. Rotating Effect of Force

Have you observed the position of the handle in a door? It is always placed at the edge of door and not at some other place. Why? Have you tried to push a door by placing your hand closer to the hinges or the fixed edge? What do you observe?

The door can be easily opened or closed when you apply the force at a point far away from the fixed edge. In this case, the effect of the force you apply is to turn the door about the fixed edge. This turning effect of the applied force is more when the distance between the fixed edge and the point of application of force is more.

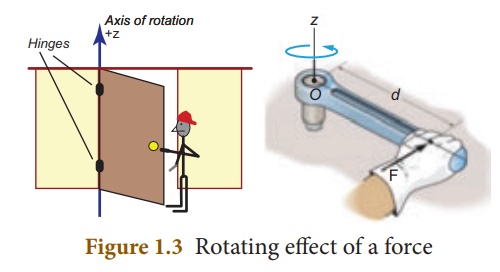
The axis of the fixed edge about which the door is rotated is called as the ‘axis of rotation’. Fix one end of a rod to the floor/wall, and apply a force at the other end tangentially.

The rod will be turned about the fixed point is called as ‘point of rotation’.

6. Moment of the Force

The rotating or turning effect of a force about a fixed point or fixed axis is called moment of the force about that point or torque (Ï„). It is measured by the product of the force (F) and the perpendicular distance (d) between the fixed point or the fixed axis and the line of action of the force. Ï„ = F × d . . . . .     (1.2)

Torque is a vector quantity. It is acting along the direction, perpendicular to the plane containing the line of action of force and the distance. Its SI unit is N m.

Couple: Two equal and unlike parallel forces applied simultaneously at two distinct points constitute a couple. The line of action of the two forces does not coincide. It does not produce any translatory motion since the resultant is zero. But, a couple results in causes the rotation of the body. Rotating effect of a couple is known as moment of a couple.

Examples: Turning a tap, winding or unwinding a screw, spinning of a top, etc.

Moment of a couple is measured by the product of any one of the forces and the perpendicular distance between the line of action of two forces. The turning effect of a couple is measured by the magnitude of its moment.

Moment of a couple = Force × perpendicular distance between th line of action of forces

M = F × S. . . . . . . . . . . . . (1.3)

The unit of moment of a couple is newton metre (N m) in SI system and dyne cm in CGS system.

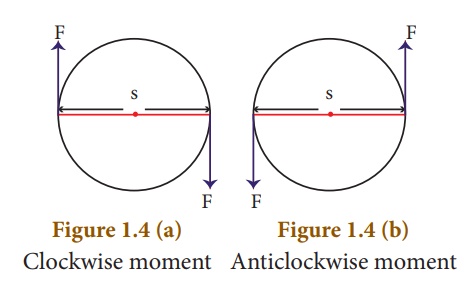
By convention, the direction of moment of a force or couple is taken as positive if the body is rotated in the anti-clockwise direction and negative if it is rotate in the clockwise direction.

They are shown in Figures 1.4 (a and b)

7. Application of Torque

1. Gears:

A gear is a circular wheel with teeth around its rim. It helps to change the speed of rotation of a wheel by changing the torque and helps to transmit power.

2. Seasaw

Most of you have played on the seasaw. Since there is a difference in the weight of the persons sitting on it, the heavier person lifts the lighter person. When the heavier person comes closer to the pivot point (fulcrum) the distance of the line of action of the force decreases. It causes less amount of torque to act on it. This enables the lighter person to lift the heavier person.

3. Steering Wheel

A small steering wheel enables you to manoeuore a car easily by transferring a torque to the wheels with less effort.

8. Principle of Moments

When a number of like or unlike parallel forces act on a rigid body and the body is in equilibrium, then the algebraic sum of the moments in the clockwise direction is equal to the algebraic sum of the moments in the anticlockwise direction. In other words, at equilibrium, the algebraic sum of the moments of all the individual forces about any point is equal to zero.

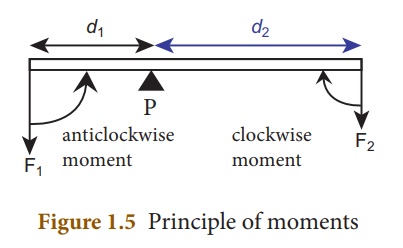
In the illustration given in figure 1.5, the force F₁ produces an anticlockwise rotation at a distance d₁ from the point of pivot P (called fulcrum) and the force F₂ produces a clockwise rotation at a distance d₂ from the point of pivot P. The principle of moments can be written as follows:

Moment in clockwise direction = Moment in anticlockwise direction

F₁ × d₁ = F₂ × d₂ . . . . . . . . . (1.4)