Gravitation

GRAVITATION

1. Newton’s universal law of gravitation

This law states that every particle of matter in this universe attracts every other particle with a force. This force is directly proportional to the product of their masses and inversely proportional to the square of the distance between the centers of these masses. The direction of the force acts along the line joining the masses.

Force between the masses is always attractive and it does not depend on the medium where they are placed.

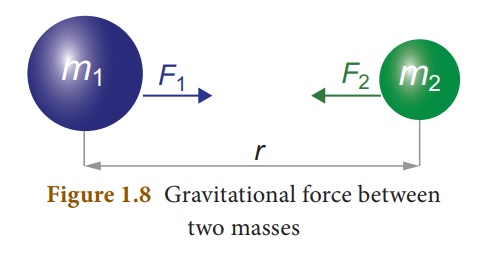
Let, m₁ and m₂ be the masses of two bodies A and B placed r metre apart in space

Force F ∝ m₁ × m₂

F ∝ 1/ r2

On combining the above two expressions

Where G is the universal gravitational constant. Its value in SI unit is 6.674 × 10^–11 m² kg^–2.

2. Acceleration due to gravity (g)

When you throw any object upwards, its velocity ceases at a particular height and then it falls down due to the gravitational force of the Earth.

The velocity of the object keeps changing as it falls down. This change in velocity must be due to the force acting on the object. The acceleration of the body is due to the Earth’s gravitational force. So, it is called as ‘acceleration due to the gravitational force of the Earth’ or ‘acceleration due to gravity of the Earth’. It is represented as ‘g’. Its unit is m s^–2

Mean value of the acceleration due to gravity is taken as 9.8 m s^–2 on the surface of the Earth. This means that the velocity of a body during the downward free fall motion varies by 9.8 m s^–1 for every 1 second. However, the value of ‘g’ is not the same at all points on the surface of the earth.

3. Relation between g and G

When a body is at rests on the surface of the Earth, it is acted upon by the gravitational force of the Earth. Let us compute the magnitude of this force in two ways. Let, M be the mass of the Earth and m be the mass of the body. The entire mass of the Earth is assumed to be concentrated at its centre. The radius of the Earth is R = 6378 km (= 6400 km approximately). By Newton’s law of gravitation, the force acting on the body is given by

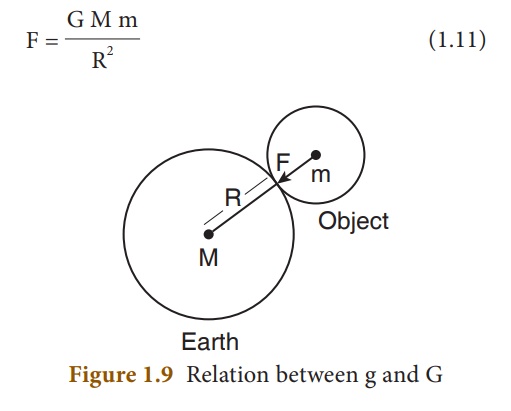
Here, the radius of the body considered is negligible when compared with the Earth’s radius. Now, the same force can be obtained from Newton’s second law of motion. According to this law, the force acting on the body is given by the product of its mass and acceleration (called as weight). Here, acceleration of the body is under the action of gravity hence a = g

4. Mass of the Earth (M)

Rearranging the equation (1.14), the mass of the Earth is obtained as follows:

Mass of the Earth M = g R²/G

Substituting the known values of g, R and G, you can calculate the mass of the Earth as

M = 5.972 × 10²⁴ kg

5. Variation of acceleration due to gravity (g):

Since, g depends on the geometric radius of the Earth, (g ∝ 1/R²), its value changes from one place to another on the surface of the Earth. Since, the geometric radius of the Earth is maximum in the equatorial region and minimum in the polar region, the value of g is maximum in the polar region and minimum at the equatorial region.

When you move to a higher altitude from the surface of the Earth, the value of g reduces. In the same way, when you move deep below the surface of the Earth, the value of g reduces. (This topic will be discussed in detail in the higher classes). Value of g is zero at the centre of the Earth.