Chapter: Modern Analytical Chemistry: Kinetic Methods of Analysis
Methods Based on Chemical Kinetics: Theory and Practice
Theory and Practice
Every chemical reaction
occurs at a finite rate and, therefore, can potentially serve as
the basis for a chemical
kinetic method of analysis. To be effective, however, the
chemical reaction must meet three conditions. First, the rate of the chemical
reac- tion must be fast enough that the analysis can be conducted
in a reasonable time, but slow enough that the reaction
does not approach
its equilibrium position
while the reagents are mixing. As a practical
limit, reactions reaching
equilibrium within 1 s are not
easily studied without
the aid of specialized equipment allowing for the rapid mixing of reactants.
A second requirement is that the rate law for
the chemical reaction
must be known for the period
in which measurements are made. In addition, the rate law should allow the kinetic
parameters of interest, such as rate constants and concen-
trations, to be easily estimated. For example, the rate law for a reaction that is first order in the concentration of the analyte,
A, is expressed as

where k is the reaction’s rate constant. As shown in Appendix 5,* the integrated form of this rate law
ln [A]t = ln [A]0 – kt
or
[A]t =
[A]0e–kt ………..13.2
provides a simple mathematical relationship between the rate
constant, the reac- tion’s elapsed time,
t, the initial concentration of analyte, [A]0, and the analyte’s concentration at time t, [A]t.
Unfortunately, most reactions of analytical interest
do not follow the simple rate laws shown in equations 13.1 and 13.2.
Consider, for example,
the following re- action between an analyte, A, and a reagent, R, to form
a product, P
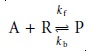
where kf is the rate constant for the forward
reaction, and kb is the rate constant for the
reverse reaction. If the forward
and reverse reactions
occur in single steps, then the rate law is
Rate = kf[A][R] – kb[P] 13.3
Although the rate law for the reaction
is known, there is no simple integrated form. We can simplify the rate law
for the reaction by restricting measurements to the beginning of the reaction
when the product’s concentration is negligible. Under these conditions, the second term in equation
13.3 can be ignored; thus
Rate = kf[A][R]
t ………..13.4
The integrated form of the rate law for equation
13.4, however, is still too compli-
cated to be analytically useful.
We can simplify the kinetics,
however, by carefully adjusting the reaction conditions.4 For example,
pseudo-first-order kinetics can be
achieved by using a large
excess of R (i.e. [R]0 >> [A]0), such that its concentration
remains essentially constant. Under these conditions
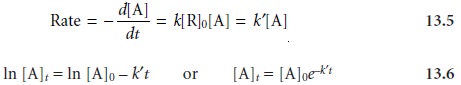
It may even be possible
to adjust conditions such that measurements are made under pseudo-zero-order conditions where
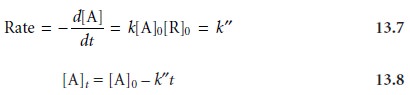
A final requirement for a chemical
kinetic method of analysis is that it must be possible to monitor the reaction’s progress
by following the change in concentra-
tion for one of the reactants or products as a function
of time. Which
species is used is
not important; thus,
in a quantitative analysis the
rate can be measured by moni-
toring the analyte, a reagent
reacting with the analyte, or a product.
For example, the concentration of phosphate can be determined by monitoring its reaction with Mo(VI) to form 12-molybdophosphoric acid
(12-MPA).
H3PO4
+ 6Mo(VI) + 9H2O → 12-MPA + 9H3O+ t ………..13.9
We can monitor
the progress of this reaction
by coupling it to a second reaction
in which 12-MPA is reduced to form heteropolyphosphomolybdenum blue,
PMB,
12-MPA + nRed → PMB + nOx
where Red is a suitable reducing agent, and
Ox is its conjugate form.5,6 The rate
of formation of PMB is measured
spectrophotometrically and is proportional to the
concentration of 12-MPA.
The concentration of 12-MPA, in turn, is proportional
to the concentration of phosphate. Reaction 13.9 also can be followed spectropho- tometrically by monitoring the formation of 12-MPA.
Classifying Chemical Kinetic Methods
A useful scheme for classifying chemical
ki- netic methods of analysis is shown in Figure 13.3. Methods are divided into two
main categories. For those methods
identified as direct-computation methods, the concentration of analyte, [A]0, is calculated using
the appropriate rate
law. Thus, for a
first-order reaction in A, equation 13.2 is used
to determine [A]0, provided that
values for k, t, and [A]t are
known. With a curve-fitting method,
regression is used to
find the best
fit between the
data (e.g., [A]t as
a function of time) and
the known mathematical model
for the rate law. In this case,
kinetic parameters, such as k and [A]0, are adjusted to find the best fit. Both categories are further subdivided into rate methods and integral methods.
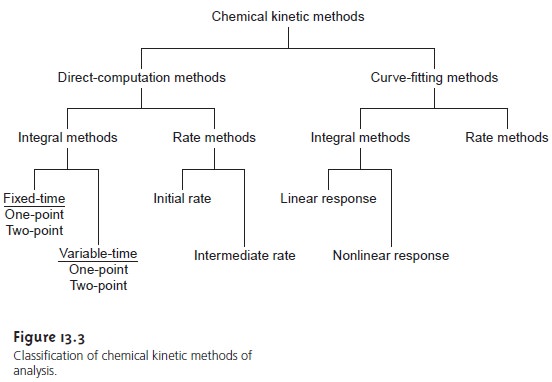
Direct-Computation Integral Methods
Integral methods for analyzing kinetic data make use of the integrated form of the rate law. In the one-point fixed-time integral method, the concentration of analyte is determined at a single time. The initial con- centration of analyte, [A]0, is calculated using
equation 13.2, 13.6,
or 13.8, depend- ing on whether the reaction follows
first-order, pseudo-first-order, or pseudo-zero-
order kinetics. The rate constant for the reaction is determined in a separate experiment using a standard
solution of analyte.
Alternatively, the analyte’s initial concentration can be determined using
a calibration curve
consisting of a plot of [A]t for several
standard solutions of known [A]0.

In Example 13.1 the initial
concentration of analyte
is determined by measur-
ing the amount of unreacted analyte at a fixed time.
Sometimes it is more conven- ient to measure the concentration of a reagent
reacting with the analyte or the con- centration of one of the reaction’s products. The one-point
fixed-time integral method can
still be applied
if the stoichiometry is known between
the analyte and the
species being monitored. For example, if the concentration of the product
in the reaction
A+R → P
is monitored, then the concentration of the analyte at time t is
[A]t =
[A]0 – [P]t ………..13.10
since the stoichiometry between the analyte
and product is 1:1. Substituting equa- tion 13.10 into equation 13.6 gives
ln([A]0 – [P]t)= ln [A]0 – k’t t ………..13.11
which is simplified by writing in exponential form
[A]0 – [P]t
= [A]0e–k’t
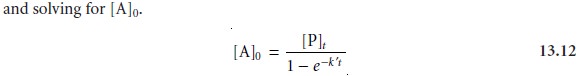

The one-point
fixed-time integral method has the advantage of simplicity since only a single
measurement is needed
to determine the analyte’s initial
con- centration. As with any method relying on a single determination, however, a one-point
fixed-time integral method cannot compensate for constant sources of
determinate error. Such corrections can be made by making measurements at two
points in time and using
the difference between
the measurements to determine the analyte’s initial concentration. Constant sources of error
affect both measurements equally, thus,
the difference between
the measurements is independent of these er- rors. For a two-point fixed-time integral method,
in which the concentration of an-
alyte for a pseudo-first-order reaction is measured at times t1 and t2, we can write
[A]t1 =
[A]0e–k’tl t ………..13.13
[A]t2 = [A]0e–k’t2

The rate constant
for the reaction
can be calculated from equation
13.14 by measur- ing [A]t1 and [A]t2 for a standard solution
of analyte. The analyte’s initial
concentra- tion also can
be found using
a calibration curve
consisting of a plot of ([A]t1 – [A]t2) versus [A]0.
Fixed-time integral methods
are advantageous for systems in which the signal is a
linear function of concentration. In this case
it is not necessary to determine the concentration of the analyte
or product at times t1 or t2, because the relevant
con- centration terms can be replaced
by the appropriate signal. For example, when a
pseudo-first-order reaction is followed spectrophotometrically, when Beer’s law
(Abs)t = εb[A]t
is valid, equations 13.6 and 13.14 can be rewritten as
(Abs)t =
[A]0(e–k’t)εb = c[A]0
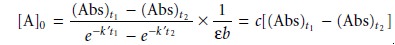
where (Abs)t is
the absorbance at time t, and c is a constant.
An alternative to a fixed-time method is a variable-time method,
in which we measure the time required for a reaction to proceed by a fixed
amount. In this
case the analyte’s initial
concentration is determined by the elapsed
time, ∆t, with a higher
concentration of analyte
producing a smaller
∆t. For this reason
variable- time integral methods
are appropriate when
the relationship between
the detector’s response and the concentration of analyte is not linear
or is unknown. In the one-
point variable-time integral
method, the time needed to cause a desired change
in concentration is measured from the start
of the reaction. With the two-point vari- able-time integral method,
the time required
to effect a change in concentration is measured.
One important application of the variable-time integral method is the quantita- tive analysis of catalysts, which is based
on the catalyst’s ability to increase the rate
of a reaction. As the initial concentration of catalyst is increased, the time needed
to reach the desired
extent of reaction
decreases. For many catalytic systems
the rela tionship between
the elapsed time,
∆t, and the initial
concentration of analyte
is
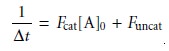
where Fcat and Funcat are constants that are functions of the rate constants for the
catalyzed and uncatalyzed reactions, and the extent
of the reaction during the time
span ∆t.
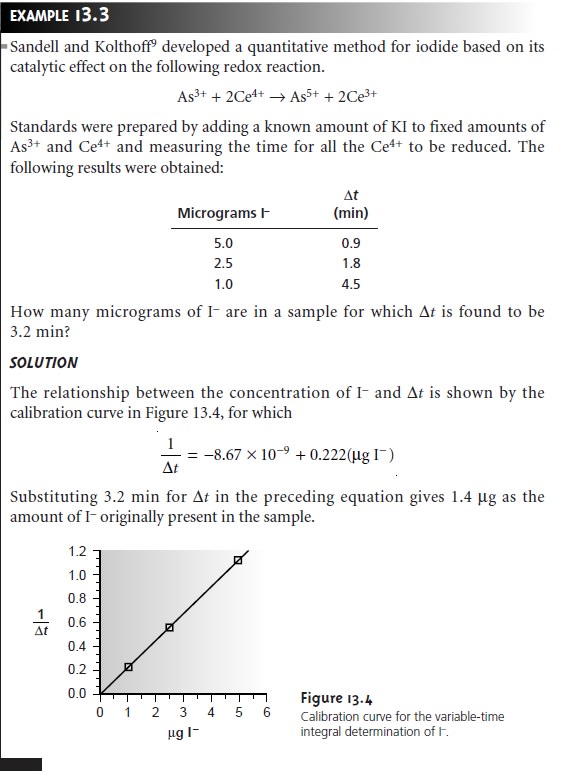
Direct-Computation Rate Methods
Rate methods for analyzing kinetic data are based on the differential form of the rate law. The rate of a reaction at time t, (rate)t, is determined from the slope of a curve showing the change in concentration for a reactant or product as a function of time (Figure 13.5).
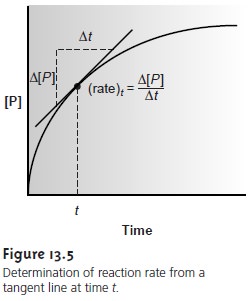
For a reaction that
is first- order, or pseudo-first-order in analyte, the
rate at time
t
is given as
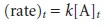
Substituting an equation
similar to 13.13
into the preceding equation gives the fol-
lowing relationship between
the rate at time t and
the analyte’s initial
concentration.
(rate)t = k[A]0e–kt
If the rate
is measured at a fixed
time, then both
k
and e–kt are constant, and a cali- bration curve of (rate)t versus [A]0 can be used for the quantitative analysis of the analyte.
The use of the initial
rate (t = 0) has the advantage that the rate is at its maxi- mum, providing an improvement in sensitivity. Furthermore, the initial rate is
measured under pseudo-zero-order conditions, in which the change in concentra-
tion with time is effectively linear, making the
determination of slope
easier. Finally, when using
the initial rate,
complications due to competing reactions are avoided. One disadvantage of the initial
rate method is that there
may be insufficient time for a complete
mixing of the reactants. This problem is avoided by using a rate mea- sured at an intermediate time (t > 0).
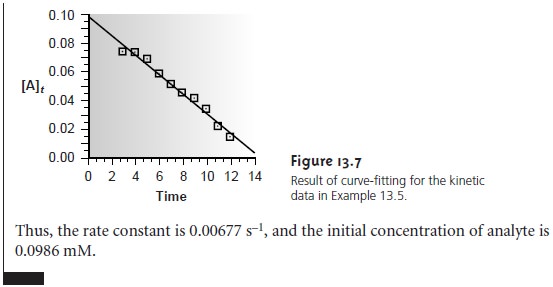
Curve-Fitting Methods
In the direct-computation methods discussed earlier,
the analyte’s concentration is determined by solving the
appropriate rate equa- tion at one or two discrete times. The relationship between the analyte’s concen- tration and the measured response is a function
of the rate constant, which must be measured in a separate
experiment. This may be accomplished using a single external
standard (as in Example 13.2)
or with a calibration curve
(as in Example 13.4).
In a curve-fitting method the concentration of a reactant or product is moni-
tored continuously as a function
of time, and a regression analysis is used to fit an
appropriate differential or integral rate equation to the data.
For example, the initial
concentration of analyte
for a pseudo-first-order reaction, in which the concentra-
tion of a product is followed as a function
of time, can be determined by fitting a re-
arranged form of equation
13.12
[P]t = [A]0(1 – e–k’t)
to
the
kinetic
data
using
both
[A]0 and k’ as adjustable parameters. By using
data from more than one or two discrete times,
curve-fitting methods are cap-
able
of producing more reliable results. Although curve-fitting methods are computationally more demanding, the calculations are easily handled
by computer.

Miscellaneous Methods
At the beginning of
this section we noted that kinetic methods are susceptible to significant errors
when experimental variables affecting the reaction’s rate
are difficult to control. Many
variables, such as temperature, can be
controlled with proper
instrumentation. Other variables, such as interferents in the sample matrix,
are more difficult to control and may lead to significant errors. Although not discussed
in this text, direct-computation and curve-fitting methods have been developed that
compensate for these
sources of error.
Representative Method
Although each chemical kinetic method has its own unique considerations, the determination of creatinine in urine based on the ki- netics of its reaction with picrate provides an instructive example of a typical procedure.
Related Topics