Line of Symmetry

Line of Symmetry

In the given figures, the red coloured line divides each figure into two equal halves and suppose we fold them along that line, we will see that one half of each figure exactly coincides with the other half. Such figures are symmetrical about that line and that line is called the line of symmetry or the axis of symmetry.

Look at the given invitation cards, the fold line of the first card divides it into two equal halves and each half exactly coincides. Hence it is a line of symmetry but in the second card, the fold line does not divide it into two equal halves. So, it is not a line of symmetry.

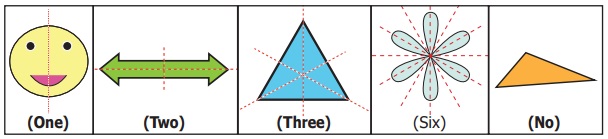
A figure may have one, two, three or more lines of symmetry or no line of symmetry.

Think

The diagonal of a rectangle divides it into two equal halves but it is not a line of symmetry. Why?

Note

The line of symmetry can be vertical, horizontal or slant.

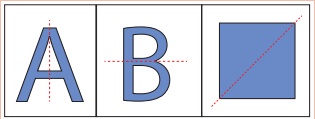
The word “symmetry” comes from the Greek word “symmetros” which means “having a common measure”.

Some examples for Symmetry

Symmetry can be found anywhere in nature as well as in man-made objects. A few of them are leaves, insects, flowers, animals, note books, bottles, architecture, designs and shapes, etc.,

We observe a few symmetrical things in our surroundings as follows.

Symmetry in Kolams

In Tamilnadu, our people usually decorate their corridors by beautiful kolams using rice flour. Those kolams look beautiful as most of them are symmetrical.

Try these

1. Is the dotted line shown in each figure a line of symmetry? If yes put ✓ otherwise put ×. Justify your answer.

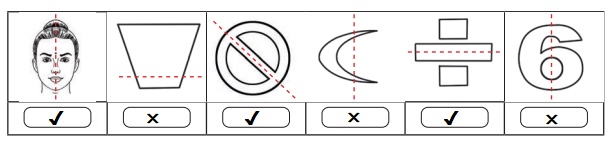
2. Check the following figures for symmetry? Write YES or NO.

Example 1

Draw the lines of symmetry for the given figures and also find the number of lines of symmetry.

 Solution:

Example 2

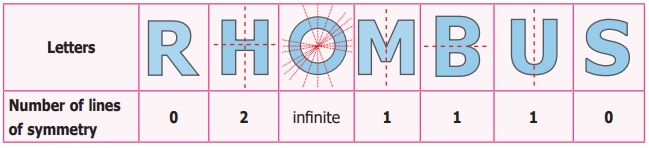
Draw the lines of symmetry for each of the letters in the word RHOMBUS and also find the number of lines of symmetry. (Note: Here the letter ‘O’ is in circle shape.)

Solution:

Example 3

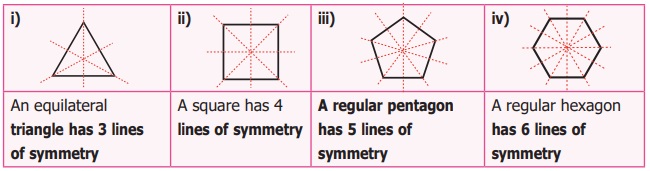
Draw the lines of symmetry for an equilateral triangle, a square, a regular pentagon and a regular hexagon and also find the number of lines of symmetry.

Solution:

Note

The number of lines of symmetry of each regular polygon (a closed figure having equal sides and equal angles) is equal to its number of sides.

Try these

1. Draw the following figures in a paper. Cut out each of them and fold so that the two parts of each figure exactly coincide.

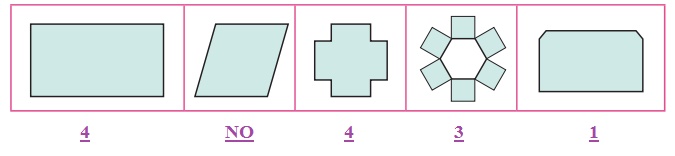
i) Which of the above figures have one, two or more lines of symmetry?

1 st, 3rd, 4th and 5th figures.

ii) Which of the above figures do not have any line of symmetry?

Parallelogram

2. Write the numbers from 0 to 9.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

i) Which numbers have a line of symmetry?

0, 1, 3, 8.

ii) List out the numbers which do not have a line of symmetry.

2, 4, 5, 6, 7, 9.

Example 4

Complete the other half of the following figures such that the dotted line is a line of symmetry.

Solution

Activity

Complete the other half of the following figures such that the dotted line is the line of symmetry.