Laser for Measurement of Distance

Laser for Measurement of Distance:

Laser-based distance measurements can be done using interferometricprinciples. Measurements of length using optical interferometry have been performed since the 19th century. But the limited intensity and coherence of conventional light sources restricted the measurements, which were difficult and suitable for used only over distances of a few centimeters. The development of lasers removed these restrictions. Lasers have allowed interferometer to develop into a fast, highly accurate and versatile technique for measuring longer distance.

Interferometric measurement of distance can be highly accurate. It offers a higher degree of precision than the pulsed time-of-flight or beam-modulation telemetry methods. However, it is best suited to measurements made in a controlled atmosphere (for example, indoors) over distances no greater than a few tens of meters.

Most laser-based interferometric systems for measurement of distance use a frequency stabilized helium-neon laser. An unstabilized laser, operating in a number of longitudinal modes, will have a total linewidth around 109 Hz. This spread in the frequency (or wavelength) will cause the interference fringes to become blurred and to lose visibility as the distance increases. An unstabilized laser is suitable for measurement only over distances of a few centimeters. Stabilized lasers, usually in a temperature-controlled environment and operating in a single longitudinal mode, are used for longer distances.

We describe first the operation of a system based on the Michelson interferometer,because it is easy to understand the basic principles of interferometer distance measurement with reference to the Michelson interferometer. Later we will describe variations that provide better stability under conditions of atmospheric turbulence.

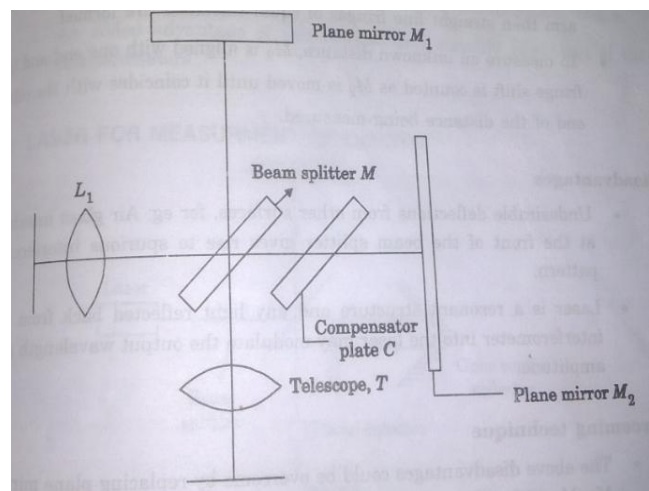
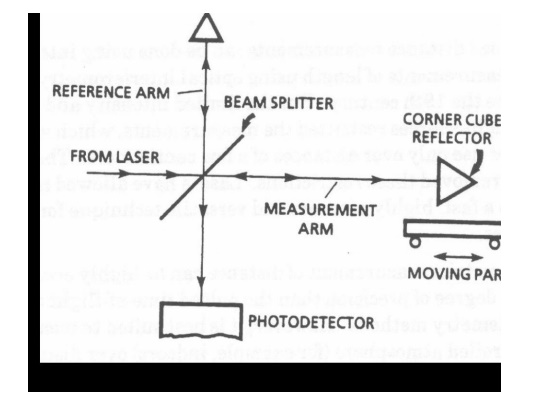
The beam from the laser falls on a beam splitter that reflects half the beam in one direction (the reference arm) and transmits the other half (the measurement arm). The two beams are each reflected by mirrors, a stationary mirror in the reference arm and a movable mirror in the measurement arm. In practice the mirrors are often cube corner reflectors (retroreflectors) which offer better stability against vibrations than conventional flat mirrors.

Schematic diagram of the application of a Michelson interferometer to measurement of distance The two reflected beams are recombined at the beam splitter to form an interference pattern

that is viewed by an observer or measured by a recorder such as a photo detector. The character of the fringes is related to the different optical path lengths traveled by the two beams before they are recombined.

Suppose, for example, that the detector is viewing a bright fringe in the interference pattern when the movable mirror is at a certain position. If the movable mirror moves a distance equal to 1/4 of the wavelength of light, the round-trip distance traversed by the light in the measurement arm will change by 1/2 wavelength, and the fringe pattern will change so that the detector now views a dark fringe. The distance mesurement thus consists of counting the number of fringe variations as the mirror moves. Each complete fringe corresponds to a phase variation equal to 2p . The variation in phase d is determined by using the equation

d = 4p D x/l

where l is the wavelength of the light,

D x is the distance that the movable mirror has moved.

It is apparent that this method offers high precision, allowing measurements of D x to be made with an accuracy of the order of a fraction of the wavelength of light.

(55)The maximum distance D x that can be measured in this way is given by: D x max = c/Dv

Where, c = velocity of light.

D v = linewidth (i.e., spread in frequency) of the laser.