Iterative Solution Using Newton-Raphson Method - Algorithm

ITERATIVE SOLUTION USING NEWTON-RAPHSON METHOD – ALGORITHM

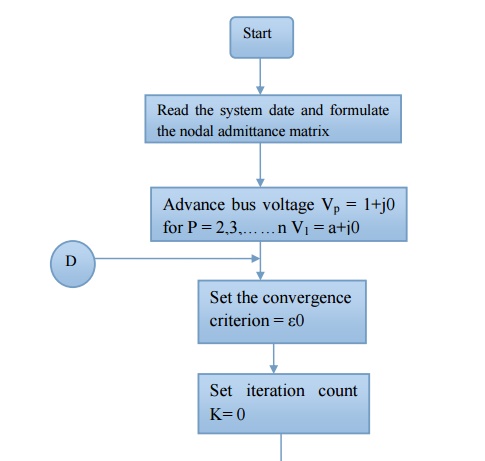
Step 1: Assume a suitable solution for all buses except the slack bus. Let Vp = a+j0 for P

= 2,3,……n V1 = a+j0

Step 2 : Set the convergence criterion = ε0

Step 3 : Set iteration count K= 0

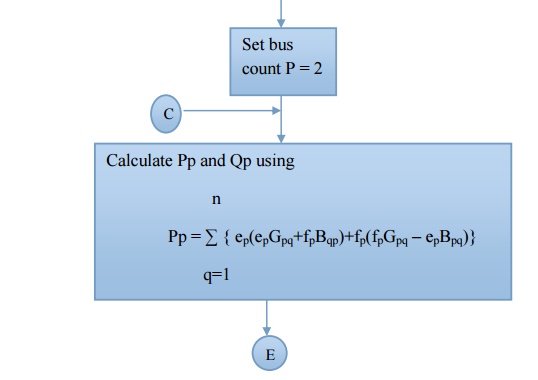
Step 4 : Set bus count P = 2

Step 5 : Calculate Pp and Qp using n

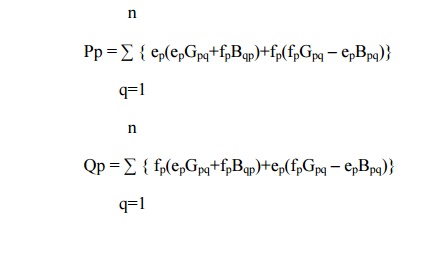
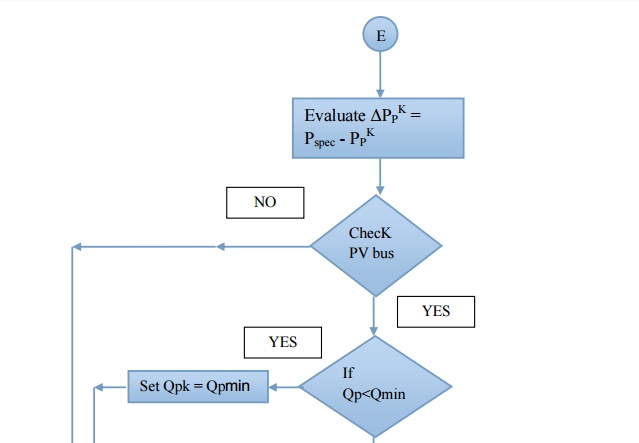
Step 6 : Evaluate ΔPPK = Pspec - PPK

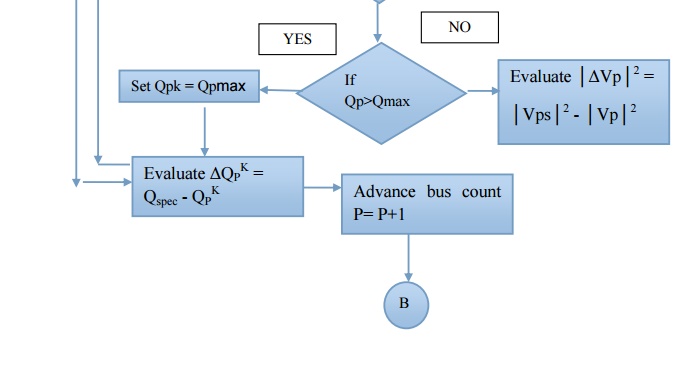
Step 7 : Check if the bus is the question is a PV bus. If yes compare QPK with the limits. If it exceeds the limit fix the Q value to the corresponding limit and treat the bus as PQ for that iteration and go to next step (or) if the lower limit is not violated evaluate │ΔVP│2 = │ Vspec│2 - │VPK│2 and go to step 9

Step 8: Evaluate ΔQPK = Qspec - QPK

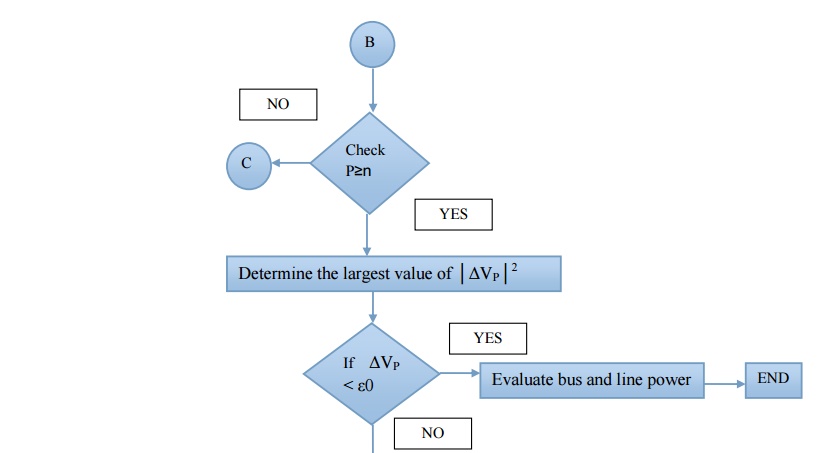
Step 9 : Advance bus count P = P+1 and check if all buses taken in to account if not go to step 5

Step 10 : Determine the largest value of │ΔVP│2

Step 11: If ΔVP < ε go to step 16

Step 12: Evaluate the element of Jacobin matrices J1, J2, J3, J4, J5 and J6

Step 13: Calculate ΔePK and ΔfPK

Step 14: Calculate ePK+1 = ePK + ΔePK and fPK+1 = fPK + ΔfPK

Step 15 : Advance count (iteration) K=K+1 and go to step 4

Step 16: Evaluate bus and line power and print the result

Iterative solution using Newton-Raphson method – Flow chart

Advantages and disadvantages of N.R method

Advantages: Faster, more reliable and results are accurate, require less number of iterations;

Disadvantages: Program is more complex, memory is more complex.