Iterative Solution Using Gauss-Seidel Method - Algorithm

ITERATIVE SOLUTION USING GAUSS-SEIDEL METHOD - ALGORITHM

Algorithm of Gauss seidal method

Step1: Assume all bus voltage be 1+ j0 except slack bus. The voltage of the slack bus is a constant voltage and it is not modified at any iteration

Step 2: Assume a suitable value for specified change in bus voltage which is used to compare the actual change in bus voltage between K th and (K+1) th iteration

Step 3: Set iteration count K = 0 and the corresponding voltages are V10, V20, V30, …… Vn0 except slack bus

Step 4: Set bus count P = 1

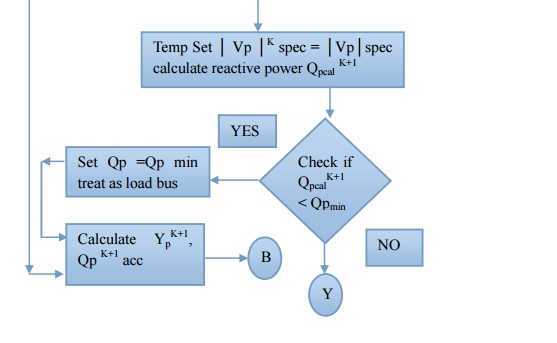
Step 5: Check for slack bus. It is a slack bus then goes to step 12 otherwise go to next step

Step 6: Check for generator bus. If it is a generator bus go to next step. Otherwise go to step 9

Step 7: Set │VPK│= │VP│ specified and phase of │VPK│ as the K th iteration value if the bus P is a generator bus where │VP│ specified is the specified magnitude of voltage for bus P. Calculate reactive power rating

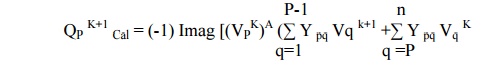
Step 8: If calculated reactive power is within the specified limits then consider the bus as generator bus and then set QP = QP K+1     Cal for this iteration go to step 10

Step 9 : If the calculated reactive power violates the specified limit for reactive power then treat this bus as load bus                        

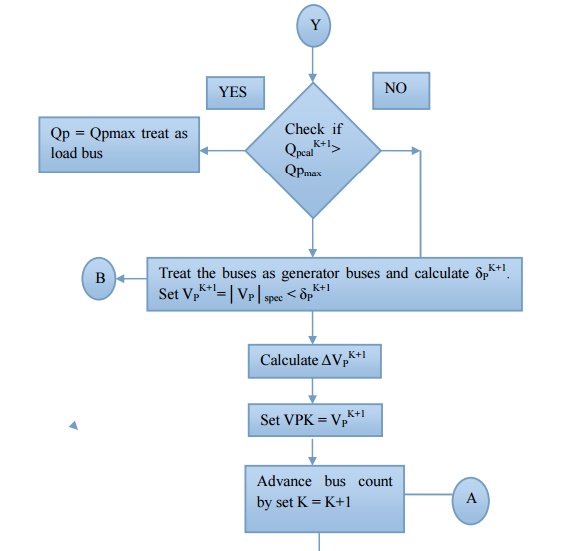
If QP K+1 Cal         <   QP min then QP = QP min

QPK+1Cal    >       QP max then QP = QP max

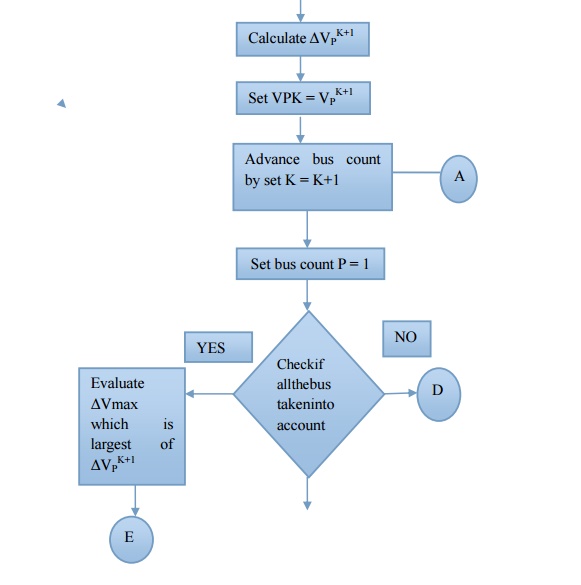
Step10: For generator bus the magnitude of voltage does not change and so for all iterations the magnitude of bus voltage is the specified value. The phase of the bus voltage can be calculated using          

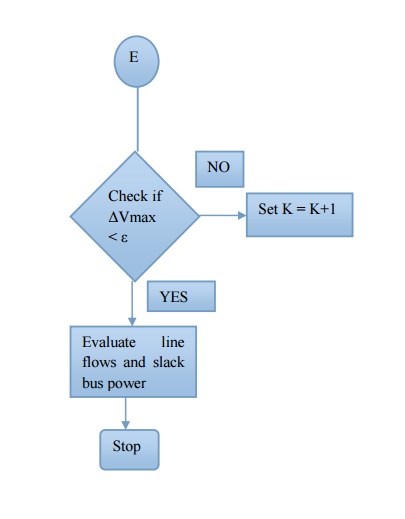
Step 16: Calculate the line flows and slack bus power by using the bus voltages

Gauss - Seidal method flow chart

Advantages and disadvantages of Gauss-Seidel method

Advantages: Calculations are simple and so the programming task is lessees. The  memory requirement is less. Useful for small systems;

Disadvantages: Requires large no. of iterations to reach converge .Not suitable for large  systems. Convergence time increases with size of the system