Chapter: Artificial Intelligence(AI) : Expert System
Inference Engine
Inference Engine
The inference engine is a generic
control mechanism for navigating through and manipulating knowledge and deduce
results in an organized manner.
The inference engine's generic
control mechanism applies the axiomatic (self-evident) knowledge present in the
knowledge base to the task-specific data to arrive at some conclusion.
Inference engine the other key
component of all expert systems.
Just a knowledge base alone is not
of much use if there are no facilities for navigating through and manipulating
the knowledge to deduce something from knowledge base.
A knowledge base is usually very
large, it is necessary to have inferencing mechanisms that sea h through the
database and deduce results in an organized manner.
The Forward chaining, Backward some
chaining and Tree sea hes are of the techniques used for drawing inferences
from the knowledge base.
1. Forward Chaining Algorithm
Forward chaining is a techniques
for drawing inferences from Rule base. Forward-chaining inference is often
called data driven.
The algorithm proceeds from a given
situation to a desired goal, adding new assertions (facts) found.
A forward-chaining, system compares
data in the working memory against the conditions in the IF parts of the rules
and determines which rule to fire.
Data Driven

‡ Example : Forward Channing
■ Given : A Rule base contains following Rule
set
Rule 1: If A and C Then F
Rule 2: If A and E Then G
Rule 3: If B Then E
Rule 4: If G Then D
■ Problem : Prove
If A
and B true Then D is true
Solution :
‡
Start with input given A, B is true and then
start at Rule 1
and go forward/down till a rule
“fires'' is found.
First iteration :
‡ Rule 3 fires : conclusion E is true
new
knowledge found
‡ No
other rule fires;
end of first
iteration.
‡ Goal
not found;
new
knowledge found at (ii);
go for
second iteration Second
iteration :
(v) ‡ Rule 2 fires :
conclusion G is true
‡ new knowledge found
(vi) ‡ Rule 4 fires :
conclusion D is true
Goal found;
Proved
2 Backward Chaining Algorithm
Backward chaining is a techniques
for drawing inferences from Rule base. Backward-chaining inference is often
called goal driven.
The algorithm proceeds from desired
goal, adding new assertions found.
A backward-chaining, system looks
for the action in the THEN clause of the rules that matches the specified goal.
Goal Driven
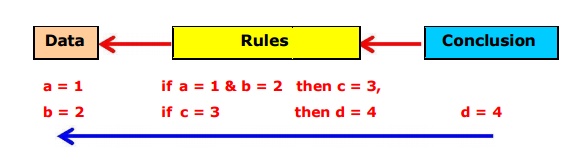
‡ Example : Backward Channing
■ Given : Rule base contains following Rule set
Rule 1: If A and C Then F
Rule 2: If A and E Then G
Rule 3: If B Then E
Rule 4: If G Then D
■ Problem : Prove
If
A and B true Then D is true
■
Solution :
(i) ‡ Start with goal ie D is true
go backward/up
till a rule "fires'' is found. First iteration :
‡ Rule 4 fires :
new sub goal
to prove G
is true
go backward
‡ Rule 2 "fires'';
conclusion: A is true
new sub goal
to prove E
is true
go backward;
‡ no
other rule fires; end of first iteration.
new sub goal
found at (iii);
go for
second iteration
Second iteration :
‡ Rule 3 fires
:
conclusion B
is true (2nd input found)
both inputs A
and B
ascertained
Proved
Often a knowledge base is
represented as a branching network or tree.
Many tree sea hing algorithms
exists but two basic approaches are depth-first sea h and breadth-first sea h.
Note : Here these two sea h are
briefly mentioned since they were described with examples in the previous
lectures.
■
Depth-First Sea h
‡ Algorithm begins at initial node
‡ Check to see if the left-most
below initial node (call node A) is a goal node.
‡ If not, include node A on a list
of sub-goals outstanding.
‡ Then starts with node A and looks
at the first node below it, and so on.
‡ If no more lower level nodes, and
goal node not reached, then start from last node on outstanding list and follow
next route of descent to the right.
■
Breadth-First Sea h
‡ Algorithm starts by expanding all
the nodes one level below the initial node.
Expand all nodes till a solution is
reached or the tree is completely expanded.
Find the shortest path from initial
assertion to a solution.
Related Topics