Important Short Objective Question and Answers: Numerical Differentiation and Integration

1. State the disadvantages of Taylor series method.

Sol:

In the differential equation = f(x,y) the function f(x,y) may have a complicated

algebraical structure. Then the evaluation of higher order derivatives may become tedious. This is the demerit of this method.

2.      Which   is   better   Taylor’s   method   or   R.K   met

Sol:

R.K methods do not require prior calculation of higher derivatives of y(x), as the Taylor method does. Since the differential equations using in application are often complicated, the

calculation of derivatives may be difficult. Also R.K formulas involve the computations of f(x,y) at various positions instead of derivatives and this function occurs in the given equation.

3. What is a predictor- collector method of solving a differential equation?

Sol:

predictor- collector methods are methods which require the values of y at xn, xn-1, xn-2,…

for computing the values of y at xn+1. We first use a formula to find the values of y at xn+1 and this is known as a predictor formula. The value of y so get is improved or corrected by another formula known as corrector formula.

4. Define a difference Quotient.

Sol:

A difference quotient is the quotient obtained by dividing the difference between two values of a function, by the difference between the two corresponding values of the independent.

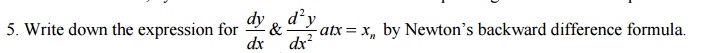
3.Find the first and second derivative of the function tabulated below at x=0.6

x        0.4     0.5     0.6     0.7     0.8

y        1.5836        1.7974        2.0442        2.3275        2.6511

4. Using Romberg’s method dxcorrectto4 decimal to places compute. Also evaluate the same integral using three –point Gauss quadrature formula. Comment on the obtained values by comparing with exact value of the integral which is equal to .

7.Evaluate I= 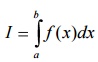   by dividing the range into ten equal parts,using                                                 

(i)Trapezoidal rule                                                                                                                                                                  

(ii)Simpson’s –third rule.

Verify one your answer with actual integration.                                                 

8. Find the first two derivatives of at x=50 and x=56, for the given table :                                      

x        50                         51                         52               53               54               55               56                  

Y=x1/3         3.6840                  3.7084                  3.7325        3.7325        3.7798        3.8030          3.8259                 

9.The velocities of a car running on a straight road at intervals of 2 minutes are given below:                  

Time(min)            0                 2                 4                 6                 8                 10               12                  

Velocity(km/hr)    0                 22               30               27               18               7                 0                  

                             rd                                                                                                                                  

Using   Simpson’s-rulefindthedistance1/3covered by the car.                                                

10. Given   the   following   data,   find   y’(6)   and   the

x        0        2        3        4        7        9

Y       4        26      58      112    466    922

Tutorial problems

Tutorial -1

1.Find the value of  f ‘’(3) using divided differences, given data

                                x     0                 1                 4        5       

                                F(x)          8                 11               68      123   

Ans:16

2.Find the first and second derivatives of the function at the point x=1.2 from the following data

X                             1     2        3        4        5

Y                             0     1        5        6        8

Ans:14.17                                        

3.A rod is rotating in a plane .The angle θ ( values of time t (seconds) are given below

t                               0     0.2     0.4     0.6     0.8     1.0     1.2

θ                              0     0.122 0.493 1.123 2.022 3.220 4.666

Find the angular velocity and angular acceleration of the rod when t=06 seconds.

Ans:6.7275 radians/sec2.

4.From the table given below ,for what value of x, y is minimum? Also find this value of y.

X                                    3                           4        5        6                 7        8                

Y                                    0.205          0.240 0.25   0.262          0.250 0.224         

Ans:5.6875,0.2628                                                                 

5.Find the first and second derivatives of y at x=500 from the following data   

x                                    500                       510    520    530             540    550            

y                                    6.2146                  6.2344        6.2538        6.2792                  6.2196                                6.3099              

Ans:0.002000,-0.0000040