Important Short Objective Question and Answers: Initial Value Problems for Ordinary Differential Equations

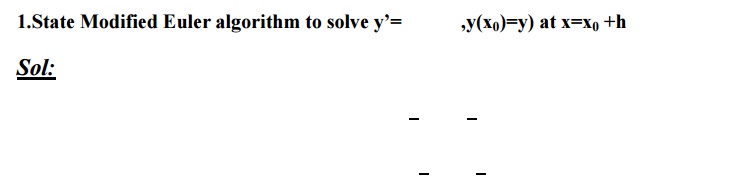
2. State the disadvantage of Taylor series method.

Sol:

In the differential equation f (x, y),   = f (x, y), the function f (x, y),may have a complicated algebraical structure. Then the evaluation of higher order derivatives may become tedious. This is the demerit of this method.

3. Write the merits and demerits of the Taylor method of solution.

Sol:

The method gives a straight forward adaptation of classic to develop the solution as an infinite series. It is a powerful single step method if we are able to find the successive derivatives easily. If f (x.y) involves some complicated algebraic structures then the calculation of higher derivatives becomes tedious and the method fails.This is the major drawback of this method. However the method will be very useful for finding the starting values for powerful methods like Runge - Kutta method, Milne’s method etc.

4.Which is better Taylor’s method or R. K. Method?(or) State the special advantage of Runge-Kutta method over taylor series method

Sol:

R.K Methods do not require prior calculation of higher derivatives of y(x) ,as the Taylor method does. Since the differential equations using in applications are often complicated, the calculation of derivatives may be difficult.

Also the R.K formulas involve the computation of f (x, y) at various positions, instead of derivatives and this function occurs in the given equation.

5.Compare Runge-Kutta methods and predictor –corrector methods for solution of initial value problem.

Sol:Runge-Kutta methods

1.Runge-methods are self starting,since they do not use information from previously calculated points.

2.As mesne are self starting,an easy change in the step size can be made at any stage. 3.Since these methods require several evaluations of the function f (x, y), they are time consuming.

4.In these methods,it is not possible to get any information about truncation error. Predictor Corrector methods:

1.These methods require information about prior points and so they are not self starting. 2.In these methods it is not possible to get easily a good estimate of the truncation error.

6. What is a Predictor-collector method of solving a differential equation?

Sol:

Predictor-collector methods are methods which require the values of y at xn,xn-1,xn-2,… for computing the value of y at . x n+1We first use a formula to find the

value of y at . x n+1 and this is known as a predictor formula.The value of y so got is improved or corrected by another formula known as corrector formula.

7. State the third order R.K method algorithm to find the numerical solution of the first order differential equation.

Sol:

To solve the differential equation y′ f (=x, y) by the third order R.K method, we use the following algorithm.