High frequency analysis of FET

High frequency analysis of FET

1. Common source amplifier at high frequencies:

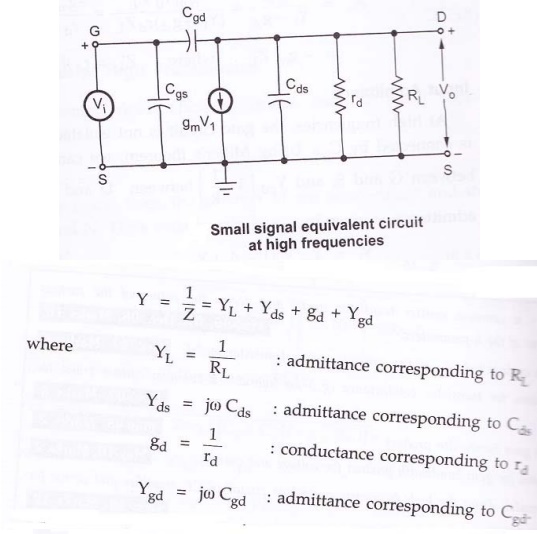
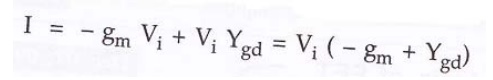
Voltage gain:

Input Admittance:

Input capacitance (Miller Effect):

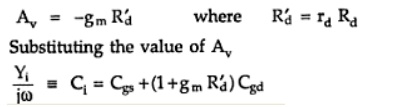
This increase in input capacitance C_i over the capacitance from gate to source is called Miller effect.

This input capacitance affects the gain at high frequencies in the operation of cascaded amplifiers. In cascaded amplifiers, the output from one stage is used as the input to a second amplifier. The input impedance of a second stage acts as a shunt across output of the first stage and R_d is shunted by the capacitance C_i.

Output Admittance:

From above figure, the output impedance is obtained by looking into the drain with the input voltage set equal to zero. If V_i = 0 in figure, r _d ,C_ds and C_gd in parallel. Hence the output admittance with R_L considered external to the amplifier is given by

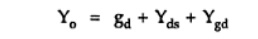
2. Common Drain Amplifier at High Frequencies:

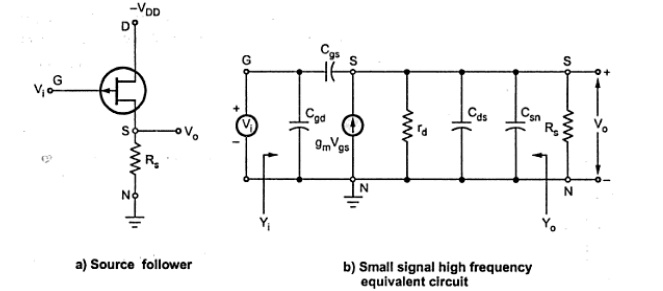
Fig. Common Drain Amplifier Circuit & Small signal equivalent circuit at high frequencies

Voltage gain:

The output voltage V_o can be found from the product of the short circuit and the impedance between terminals S and N. Voltage gain is given by,

Input Admittance:

Input Admittance Y_i can be obtained by applying Miller’s theorem to C_gs.

It is given by,

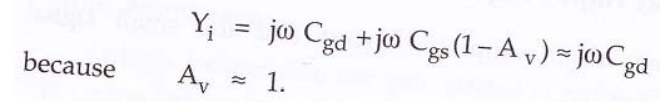
Output Admittance:

Output Admittance Y_o with R_s considered external to the amplifier, it is given by

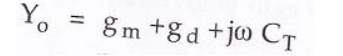
At low frequencies, output resistance R_o is given by,

3. Frequency Response of Common Source Amplifier:

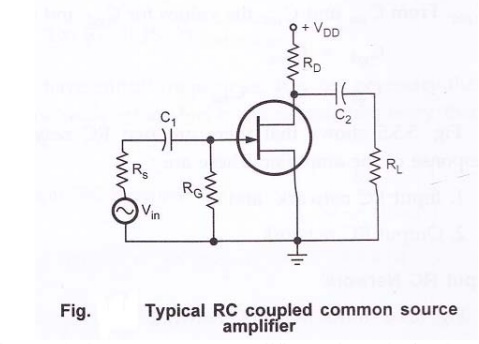
Let us consider a typical common source amplifier as shown in the above figure.

From above figure, it shows the high frequency equivalent circuit for the given amplifier circuit. It shows that at high frequencies coupling and bypass capacitors act as short circuits and do not affect the amplifier high frequency response. The equivalent circuit shows internal capacitances which affect the high frequency response.

Using Miller theorem, this high frequency equivalent circuit can be further simplified as follows:

The internal capacitance C_gd can be splitted into C_in(miller) and C_out(miller) as shown in the following figure.

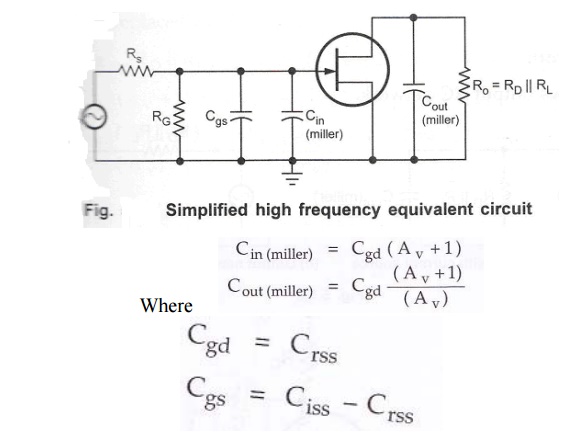
From simplified high frequency equivalent circuit, it has two RC networks which affect the high frequency response of the amplifier. These are,

·        Input RC network

·        Output RC network

Input RC network:

Fig. Input RC network

From above figure,

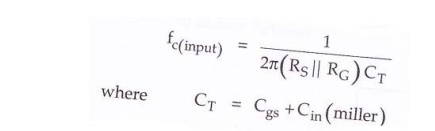
This network is further reduced as follows since R_s<< R_G

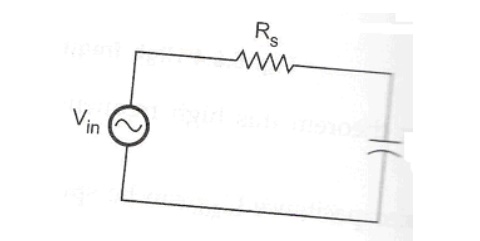
Fig. Reduced input RC network

The critical frequency for the reduced input RC network is,

Output RC network:

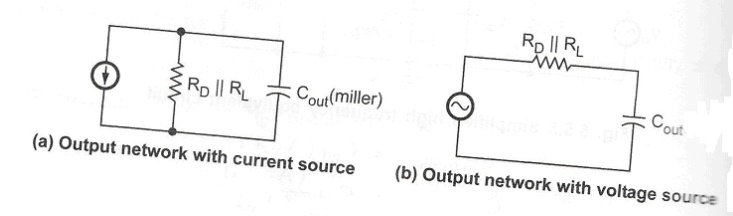
Fig. Output RC network

The critical frequency for the above circuit is,

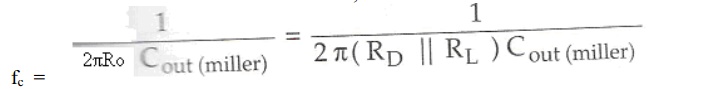
It is not necessary that these frequencies should be equal. The network which has lower critical frequency than other network is called dominant network.

The phase shift in high frequency is

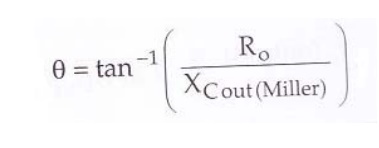
Problem:

Determine the high frequency response of the amplifier circuit shown in the following figure.

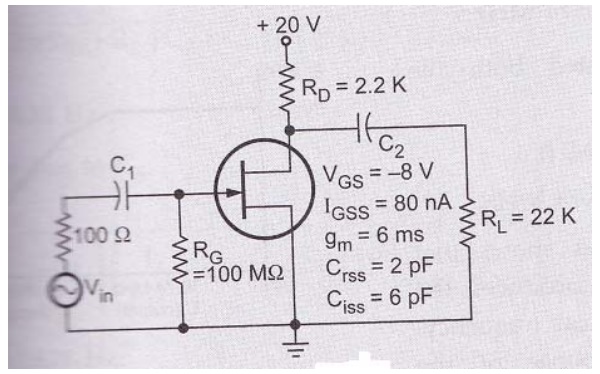
Solution:

Before calculating critical frequencies it is necessary to calculate mid frequency gain of

the given amplifier circuit. This is required to calculate C_in(miller) and C_out(miller).

A_v = -g_mR_D

Here R_D should be replaced by R_D || R_L A_v=

C_gs = C_iss – C_rss = 4pF

Now analyze the input and output network for critical frequency,

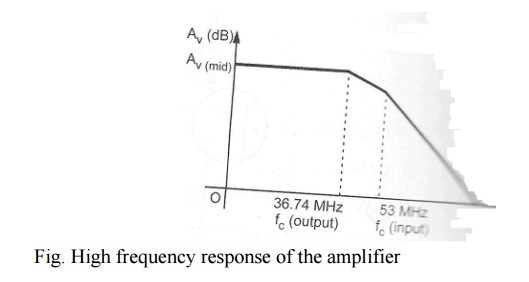
The above analysis shows that the output network produces the dominant higher critical frequency. High frequency response of the given amplifier is shown in the following figure