Mathematics - Geometry Basics ŌĆō Recall | 9th EM Mathematics : Geometry
Chapter: 9th EM Mathematics : Geometry
Geometry Basics ŌĆō Recall
Geometry Basics ŌĆōRecall
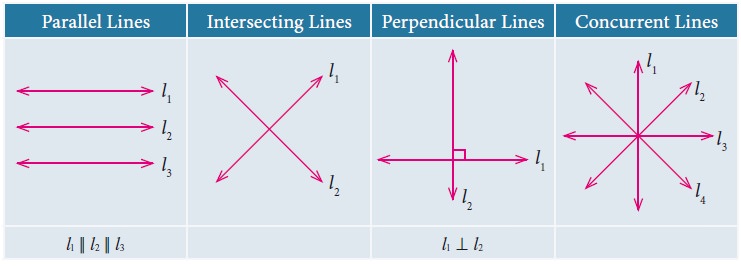
Draw two lines on a plane. They can be either
parallel or intersecting.
Parallel
lines Two or more lines lying in
the same plane that never meet.
Intersecting
lines Two lines which meet at a common
point.
Perpendicular
lines Two lines which intersect each other at right angle.
Concurrent
lines Three or more lines passing
through the same point.
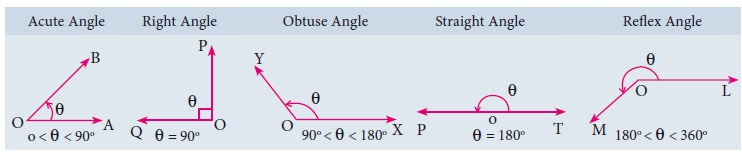
1. Types of Angles
Plumbers measure the angle between connecting pipes
to make a good fitting. Wood workers adjust their saw blades to cut wood at the
correct angle. Air Traffic Controllers (ATC) use angles to direct planes. Carom
and billiards players must know their angles to plan their shots. An angle is
formed by two rays that share a common end point provided that the two rays are
non-collinear.
Complementary Angles
Two angles are Complementary if their sum is 90┬░.
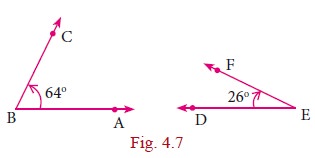
For example, if ŌłĀABC=64┬░ and ŌłĀDEF=26┬░, then angles ŌłĀABC and ŌłĀDEF are complementary to each other
because ŌłĀABC + ŌłĀDEF = 90┬░
Supplementary Angles
Two angles are Supplementary if their sum is 180┬░.
For example if ŌłĀABC=110┬░ and ŌłĀXYZ=70┬░
Here ŌłĀABC + ŌłĀXYZ = 180┬░
Ōł┤ŌłĀABC and ŌłĀXYZ are supplementary to each other
Adjacent Angles
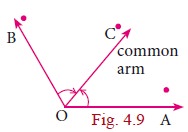
Two angles are called adjacent angles if
i. They have a common vertex
ii. They have a common arm.
iii. The common arm lies between the two non-common arms.
Linear Pair of Angles
If a ray stands on a straight line then the sum of
two adjacent angle is 180┬░. We then say that the angles so formed is a linear
pair.
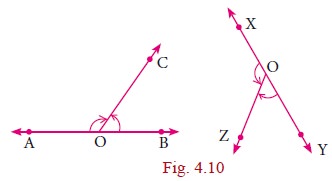
ŌłĀAOC + ŌłĀBOC=180┬░
Ōł┤ŌłĀAOC and ŌłĀBOC form a linear pair
ŌłĀXOZ + ŌłĀYOZ = 180┬░
ŌłĀXOZ and ŌłĀYOZ form a linear pair
Vertically Opposite Angles
If two lines intersect each other, then vertically
opposite angles are equal.
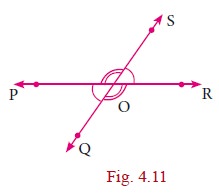
In this figure ŌłĀPOQ = ŌłĀSOR
ŌłĀPOS = ŌłĀQOR
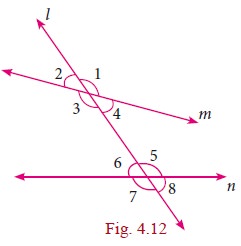
2. Transversal
A line which intersects two or more lines at a
distinct points is called a transversal of those lines.
Case (i) When a
transversal intersect two lines, we get eight angles.
In the figure the line l is the transversal for the lines m and n
(i) Corresponding Angles: ŌłĀ1 and ŌłĀ5, ŌłĀ2 and ŌłĀ6, ŌłĀ3 and ŌłĀ7, ŌłĀ4 and ŌłĀ8
(ii) Alternate Interior Angles: ŌłĀ4 and ŌłĀ6, ŌłĀ3 and ŌłĀ5
(iii) Alternate Exterior Angles: ŌłĀ1 and ŌłĀ7, ŌłĀ2 and ŌłĀ8
(iv) ŌłĀ4 and ŌłĀ5,ŌłĀ3 and ŌłĀ6 are interior angles on the same
side of the transversal.
(v) ŌłĀ1 and ŌłĀ8, ŌłĀ2 and ŌłĀ7 are exterior angles on the same
side of the transversal.
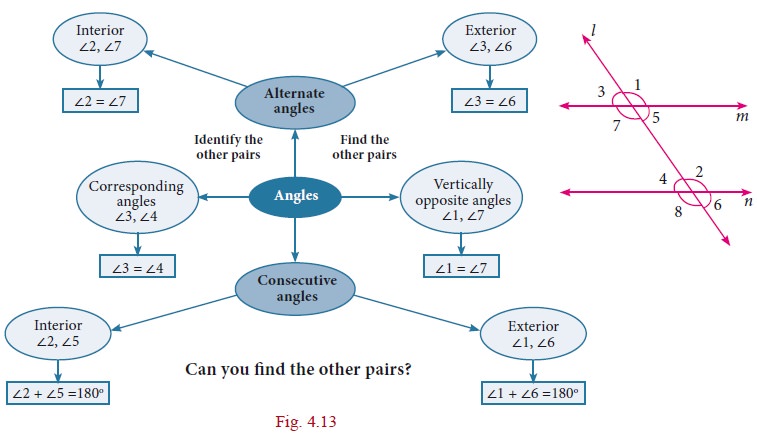
Case (ii) If a
transversal intersects two parallel lines. The transversal forms different
pairs of angles.
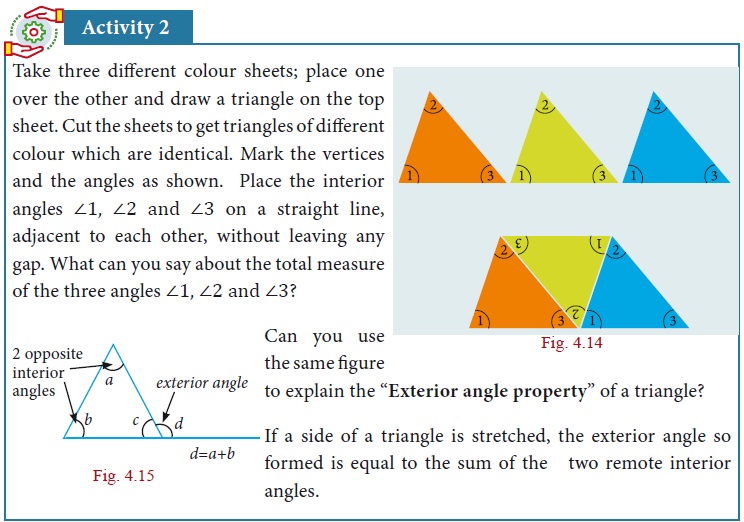
3. Triangles
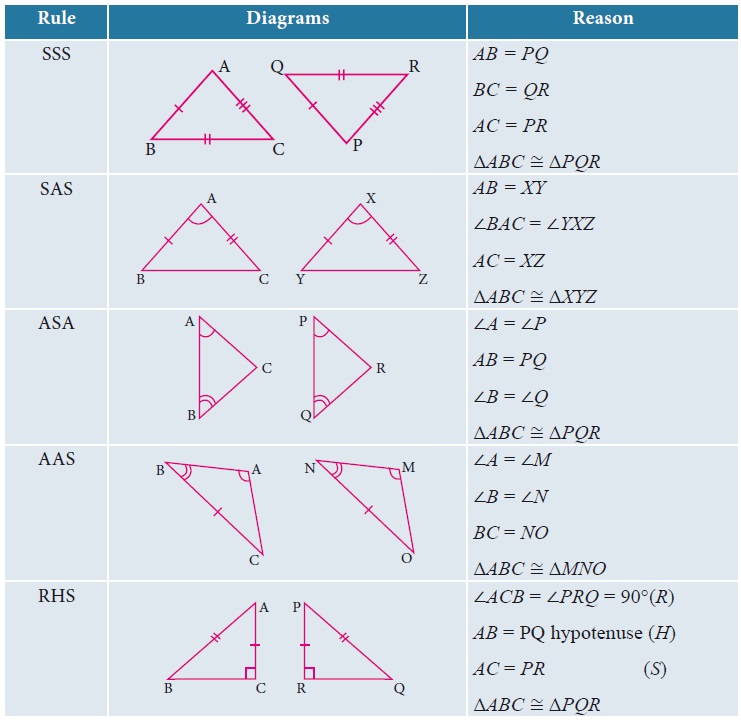
4. Congruent Triangles
Two triangles are congruent if the sides and angles
of one triangle are equal to the corresponding sides and angles of another
triangle.