Constructions

Constructions

Practical Geometry is the method of applying the rules of Geometry dealt with the properties of Points, Lines and other figures to construct geometrical figures. “Construction” in Geometry means to draw shapes, angles or lines accurately. The geometric constructions have been discussed in detail in Euclid’s book ‘Elements’. Hence these constructions are also known as Euclidean constructions. These constructions use only compass and straightedge (i.e. ruler). The compass establishes equidistance and the straightedge establishes collinearity. All geometric constructions are based on those two concepts.

It is possible to construct rational and irrational numbers using straightedge and a compass as seen in Chapter II. In 1913 the Indian mathematical Genius, Ramanujan gave a geometrical construction for 355/113 =π. Today with all our accumulated skill in exact measurements. It is a noteworthy feature that lines driven through a mountain meet and make a tunnel.In the earlier classes, we have learnt the construction of angles and triangles with the given measurements.

In this chapter we learn to construct Circumcentre and Orthocentre of a triangle by using concurrent lines.

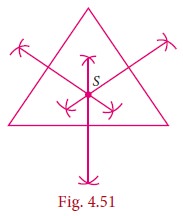
1. Construction of the Circumcentre of a Triangle Circumcentre

The Circumcentre is the point of concurrency of the Perpendicular bisectors of the sides of a triangle.

It is usually denoted by S.

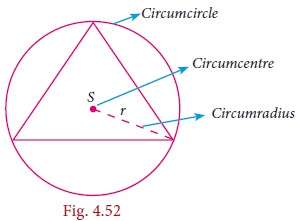
Circumcircle

The circle passing through all the three vertices of the triangle with circumcentre (S) as centre is called circumcircle.

Circumradius

The line segment from any vertex of a triangle to the Circumcentre of a given triangle is called circumradius of the circumcircle.

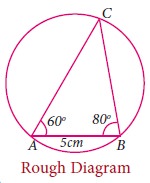
Example 4.5

Construct the circumcentre of the ΔABC with AB = 5 cm, +A = 60° and +B = 80° draw the circumcircle and find the circumradius of the ΔABC.

Solution

Step 1 Draw the ΔABC with the given measurements

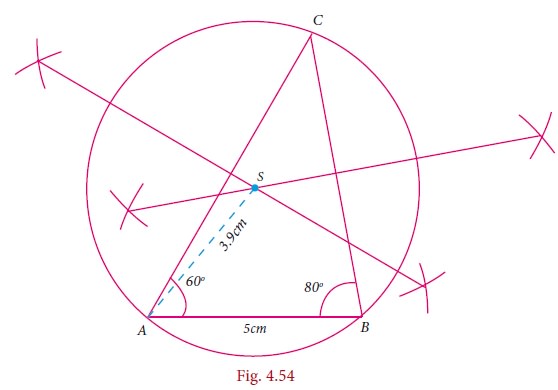
Step 2

Construct the perpendicular bisector of any two sides (AC and BC) and let them meet at S which is the circumcentre.

Step 3

S as centre and SA = SB = SC as radius,

draw the Circumcircle to passes through A,B and C.

Circumradius = 3.9 cm.

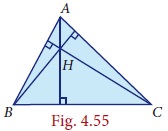
2. Construction of Orthocentre of a Triangle

Orthocentre

The orthocentre is the point of concurrency of the altitudes of a triangle. Usually it is denoted by H.

Example 4.6

Construct ΔPQR whose sides are PQ = 6 cm ∠Q = 60^o and QR = 7 cm and locate its Orthocentre.

Solution

Step 1 Draw the ΔPQR with the given measurements.

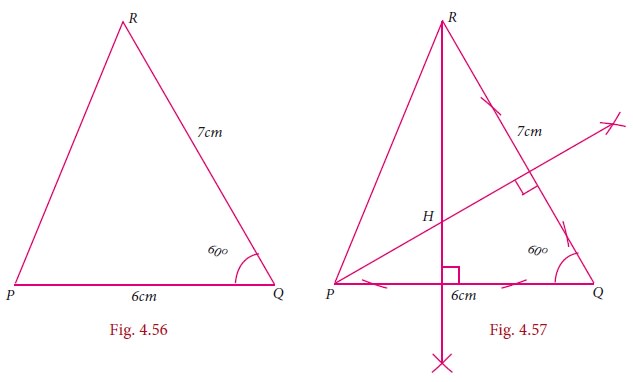
Step 2:

Construct altitudes from any two vertices R and P, to their opposite sides PQ and QR respectively.

The point of intersection of the altitude H is the Orthocentre of the given ΔPQR.