Functions and their graphs

Functions and their graphs

Some basic concepts

1. Quantity

Anything which can be performed on basic mathematical operations like addition, subtraction, multiplication and division is called a quantity.

2. Constant

A quantity which retains the same value throughout a mathematical investigation is called a constant.

Basically constant quantities are of two types

 (i). Absolute constants are those which do not change their values in any mathematical investigation. In other words, they are fixed for ever.

Examples: 3, √3 , p, ...

(ii) Arbitrary constants are those which retain the same value throughout a problem, but we may assign different values to get different solutions. The arbitrary constants are usually denoted by the letters a, b, c, ...

Example: In an equation y=mx+4, m is called arbitrary constant.

3. Variable

A variable is a quantity which can assume different values in a particular problem. Variables are generally denoted by the letters x, y, z, ...

Example: In an equation of the straight line

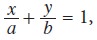
x and y are variables because they assumes the co-ordinates of a moving point in a straight line and thus changes its value from point to point. a and b are intercept values on the axes which are arbitrary.

There are two kinds of variables

i. A variable is said to be an independent variable when it can have any arbitrary value.

ii. A variable is said to be a dependent variable when its value depend on the value assumed by some other variable.

Example: In the equation y = 5x2 - 2x + 3,

“x” is the independent variable,

“y” is the dependent variable and

“3” is the constant.

4. Intervals

The real numbers can be represented geometrically as points on a number line called real line. The symbol R denotes either the real number system or the real line. A subset of the real line is an interval. It contains atleast two numbers and all the real numbers lying between them.

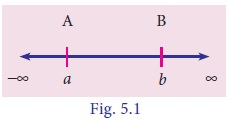
(i) Open interval

(ii) Closed interval

5. Neighbourhood of a point

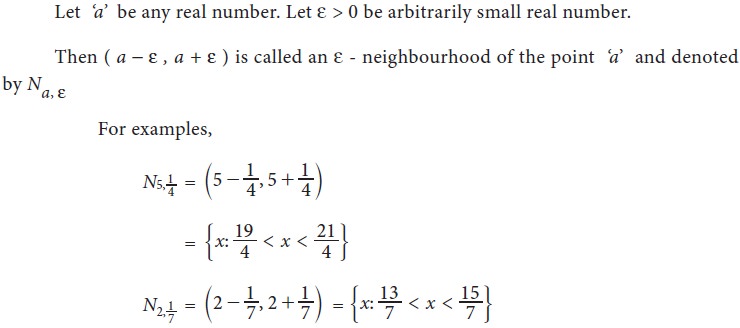
6. Function

L et X and Y be two non-empty sets of real numbers. If there exists a rule f which associates to every element x Î X, a unique element y Î Y, then    such a rule f is called a function (or mapping) from the set X to the set Y. We write f : X -- >Y.

The set X is called the domain of f, Y is called the co-domain of f and the range of f is defined as f(X) = {f(x) / x Î X}. Clearly f(X) ÍY.

A function of x is generally denoted by the symbol f(x), and read as “function of x” or “f of x”.

7. Classification of functions

Functions can be classified into two groups.

i. Algebraic functions

Algebraic functions are algebraic expressions using a finite number of terms, involving only the algebraic operations addition, subtraction, multiplication, division and raising to a fractional power.

8. Even and odd functions

A function f(x) is said to be an even function of x, if f( - x ) = f( x ).

A function f(x) is said to be an odd function of x, if f( - x ) = - f( x ).

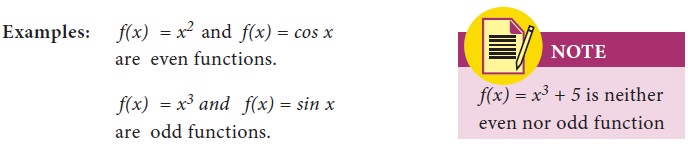
9. Explicit and implicit functions

A function in which the dependent variable is expressed explicitly in terms of some independent variables is known as explicit function.

Examples: y = x2 + 3 and  y = ex + e-x are explicit functions of x.

If two variables x and y are connected by the relation or function f(x, y) = 0 and none of the variable is directly expressed in terms of the other, then the function is called an implicit function.

Example: x3 + y3-xy = 0 is an implicit function.

10. Constant function

If k is a fixed real number then the function given by f(x) = k for all x Î R is called a constant function.

Examples: y = 3, f(x) = –5 are constant functions.

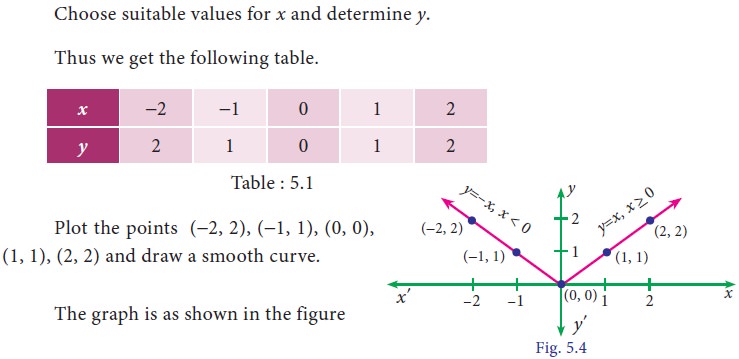
11. Identity function

A function that associates each real number to itself is called the identity function and is denoted by I.

i.e. A function defined on R by f(x) = x for all x ∈ R is an identity function.

Example: The set of ordered pairs {(1, 1), (2, 2), (3, 3)} defined by f : A -> A where A={1, 2, 3} is an identity function.

12. Modulus function

13. Signum function

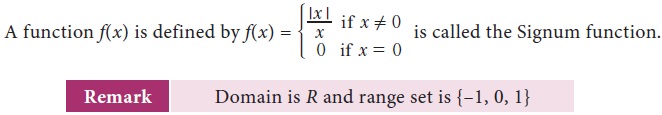
14. Step function

(i) Greatest integer function

The function whose value at any real number x is the greatest integer less than or equal to x is called the greatest integer function. It is denoted by x .

i.e. f : R -> R defined by f(x) =   ëxû is called the greatest integer function.

(ii) Least integer function

The function whose value at any real number x is the smallest integer greater than or equal to x is called the least integer function. It is denoted by x .

i.e. f : R à R defined by f(x) = é x ù is called the least integer function

Remark : Function’s domain is R and range is Z [set of integers]

15. Rational function

16. Polynomial function

For the real numbers a0, a1, a2, ..., an ; a0 ¹ 0 and n is a non-negative integer, a function f(x) given by f] xg = a0 xn + a1 xn - 1 + a2 xn - 2 + ... + an is called as a polynomial function of degree n.

Example: f (x ) = 2x 3 + 3x2 + 2x - 7 is a polynomial function of degree 3.

17. Linear function

For the real numbers a and b with a ¹ 0, a function f(x) = ax + b is called a linear function.

Example: y = 2x + 3 is a linear function.

18. Quadratic function

For the real numbers a, b and c with a ¹ 0, a function f(x) = ax2 + bx + c is called a quadratic function.

Example: f (x ) = 3x2 + 2x - 7 is a quadratic function.

19. Exponential function

A function f(x) = ax, a ¹ 1 and a > 0, for all x ∈ R is called an exponential function

Remark : Domain is R and range is (0, ∞) and (0, 1) is a point on the graph

Examples: e2x , ex2 + 1 and 2x are exponential functions.

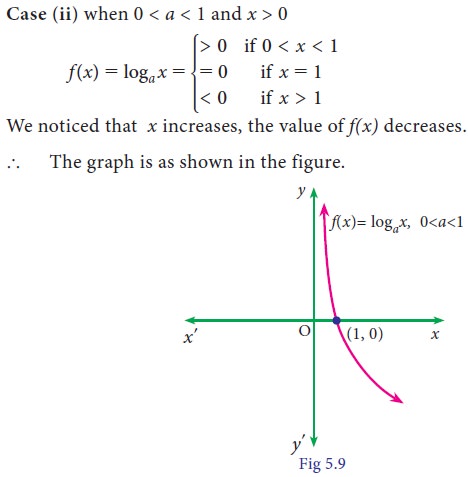
20. Logarithmic function

For x > 0, a > 0 and a ¹1, a function f(x) defined by f(x) = logax is called the logarithmic function.

Remark: Domain is (0, ∞), range is R and (1, 0) is a point on the graph

Example: f(x) = loge(x+2), f(x) = loge (sinx) are logarithmic functions.

21. Sum, difference, product and quotient of two functions

22. Graph of a function

T he graph of a function is the set of points (x , f(x)) where x belongs to the domain of the function and f(x) is the value of the function at x.

To draw the graph of a function, we find a sufficient number of ordered pairs (x , f(x)) belonging to the function and join them by a smooth curve.