Formula, Solved Example Problems, Exercise | Differential Calculus | Mathematics - Differentiation techniques | 11th Business Mathematics and Statistics(EMS) : Chapter 5 : Differential Calculus
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 5 : Differential Calculus
Differentiation techniques
Differentiation techniques
In this section we will discuss about different techniques to obtain the derivatives of the given functions.
1. Some standard results [formulae]
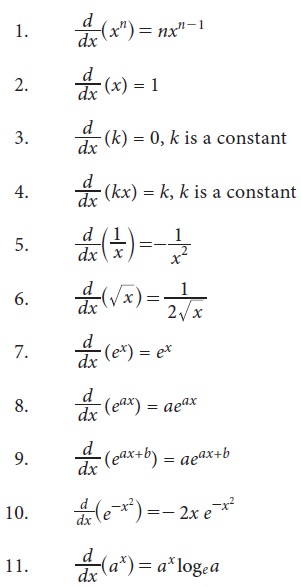
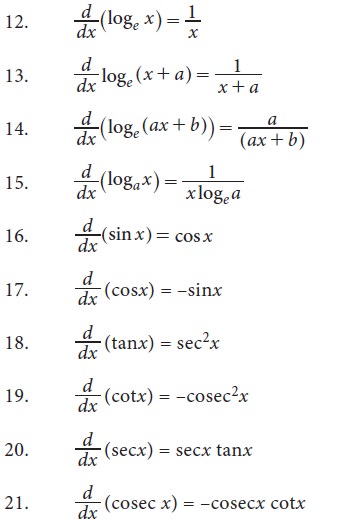
2. General rules for differentiation
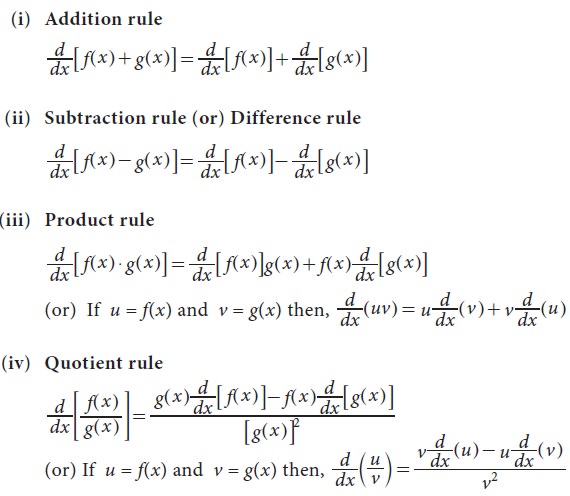


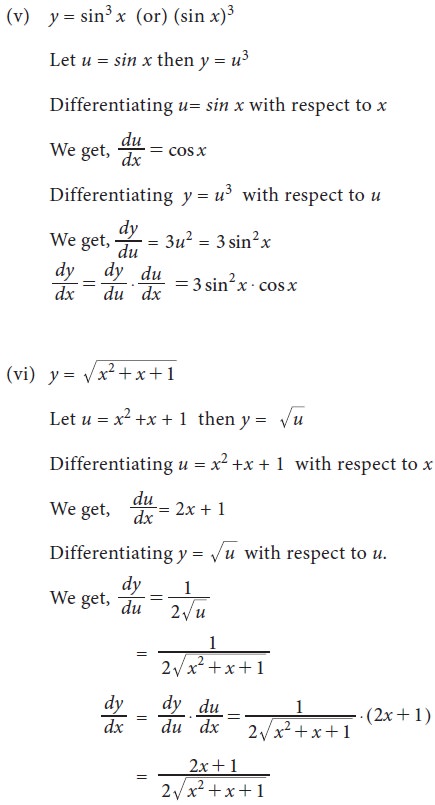


3. Derivative of implicit functions
For the implicit function f(x,y) = 0, differentiate each term with respect to x treating y as a function of x and then collect the terms of dy/dx together on left hand side and remaining terms on the right hand side and then find dy/dx.
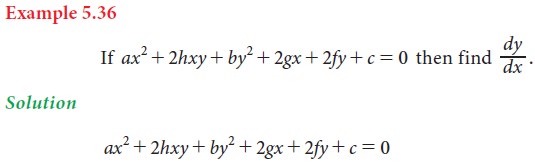




4. Logarithmic differentiation
Some times, the function whose derivative is required involves products, quotients, and powers. For such cases, differentiation can be carried out more conveniently if we take logarithms and simplify before differentiation.



5. Differentiation of parametric functions
If the variables x and y are functions of another variable namely t, then the functions are called a parametric functions. The variable t is called the parameter of the function.
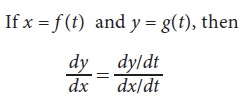
6. Differentiation of a function with respect to another function
Let u = f(x) and v = g(x) be two functions of x. The derivative of f(x) with respect to g(x) is given by the formula,
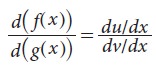




7. Successive differentiation
The process of differentiating the same function again and again is called successive differentiation.

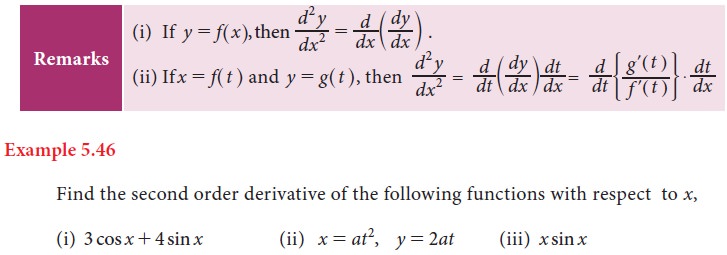



Related Topics