Chapter: Control Systems : Frequency Response Analysis
Frequency Response
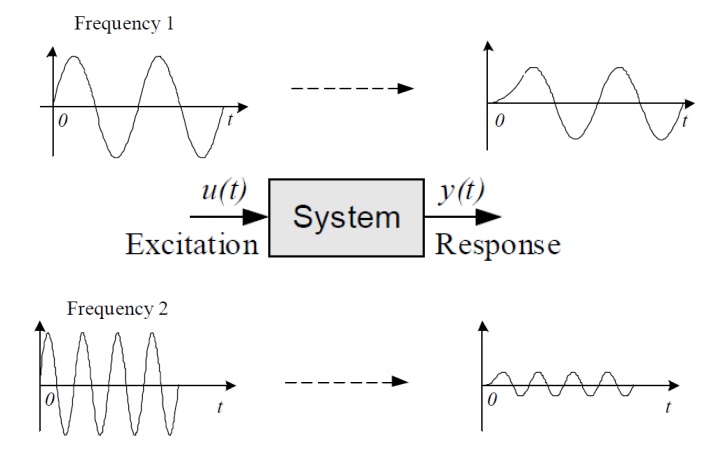
Frequency Response
The
frequency response of a system is a frequency dependent function which
expresses how a sinusoidal signal of a given frequency on the system input is
transferred through the system. Time-varying signals at least periodical
signals —which excite systems, as the reference (set point) signal or a
disturbance in a control system or measurement signals which are inputs signals
to signal filters, can be regarded as consisting of a sum of frequency
components. Each frequency component is a sinusoidal signal having certain
amplitude and a certain frequency. (The Fourier series expansion or the Fourier
transform can be used to express these frequency components quantitatively.)
The frequency response expresses how each of these frequency components is
transferred through the system. Some components may be amplified, others may be
attenuated, and there will be some phase lag through the system.
The
frequency response is an important tool for analysis and design of signal
filters (as low pass filters and high pass filters), and for analysis, and to
some extent, design, of control systems. Both signal filtering and control
systems applications are described (briefly) later in this chapter. The
definition of the frequency response — which will be given in the next section
— applies only to linear models, but this linear model may very well be the
local linear model about some operating point of a non-linear model. The
frequency response can found experimentally or from a transfer function model.
It can be presented graphically or as a mathematical function.
Related Topics