Information Processing | Term 3 Chapter 5 | 6th Maths - EuclidŌĆÖs game | 6th Maths : Term 3 Unit 5 : Information Processing
Chapter: 6th Maths : Term 3 Unit 5 : Information Processing
EuclidŌĆÖs game
EuclidŌĆÖs
game
Ammu and Balu are playing a game. Each one can choose
any number and they write it down on a piece of paper. If Ammu picks up the number
greater than what Balu picked up, then Ammu will find the difference of the two
numbers. That difference will be shown to Balu. Now Balu takes the chance to find
the difference between the number what he has and the number shown to him by Ammu.
They will continue the process until the difference and the numbers they have become
equal. Finally, the person who gets the number equal to the difference wins the
game Let us see how it works
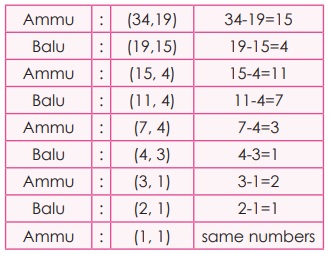
Suppose Ammu picked the number 34 and Balu picked
the number 19. Ammu first finds the difference between 34 and 19 which gives 15.
She shows the difference to Balu. Now Balu has 19 and she has 15, the difference
is 4. He shows to Ammu and so on. (the bigger number should be kept first to find
the difference). So Ammu wins.
Now suppose they start with Ammu (24, 18).
It goes: (24, 18) ŌåÆ (18, 6) Ammu ŌåÆ (12, 6) Balu ŌåÆ (6, 6) Ammu. Ammu wins again!
If they start
with Ammu (18, 6), we get (18, 6) ŌåÆ (12, 6) ŌåÆ (6, 6) Balu wins!
Play the game with your friends and see for what
pairs of numbers the first player (Ammu ) wins, and when the second player wins.
Now we can notice something interesting! Begin with
any pair of numbers. Can you say anything about the pair of numbers. Remember that
we stop the process when both the numbers are same. It is the Highest Common Factor
(HCF) of the two numbers we started with. So what we have seen here is an iterative
process which leads us to the HCF of two given numbers. The HCF of a and
b (here a>b) is the same as for a and a-b.
Example 1
Find the HCF of two numbers 16 and 28.
Solution
Now the HCF of 16, 28
16 = 2 ├Ś 2 ├Ś 2 ├Ś 2
28 = 2 ├Ś 2 ├Ś 7
HCF of (16, 28) = 2 ├Ś 2 = 4
Now the HCF of (16 , 28-16)
16 = 2 ├Ś 2 ├Ś 2 ├Ś 2
12 = 2 ├Ś 2 ├Ś 3
HCF of (16, 12) = 2 ├Ś 2 = 4
Therefore HCF of (16, 28) = HCF of (16, 28-16).
Hence, HCF of two numbers a and b, a > b, is
same as the HCF of a and a ŌĆō b.
Euclidean algorithm
Let us take a number 12.
If we divide 12 by 7 then, we get
quotient=1, remainder=5 and 12 can be written as 12 = (1 ├Ś 7) + 5.
If we divide 12 by 2 then, we get
quotient=6, remainder=0 and 12 can be written as 12 = (2 ├Ś 6) + 0.
From this, we observe that, if a number
ŌĆśaŌĆÖ is divided by some number ŌĆśbŌĆÖ then we get the quotient ŌĆśqŌĆÖ
and remainder ŌĆśrŌĆÖ, and ŌĆśaŌĆÖ can be written in a unique way as a
= (b ├Ś q) + r. That is, Dividend = (Divisor ├Ś Quotient) + Remainder.
This is called the Euclidean algorithm.
Related Topics