Drug Concentration-Time Profiles and Basic Pharmacokinetic Parameters

DRUG CONCENTRATION–TIME PROFILES AND BASIC PHARMACOKINETIC PARAMETERS

The time course of a drug in the body is frequently rep-resented as a concentration–time profile in which the concentrations of a drug in the body are measured ana-lytically and the results plotted in semilogarithmic form against time. A representative profile of a drug given in-travenously is presented in Figure 5.1. Drug concentra-tions are measured in samples typically taken from the brachial vein, since this vein is readily accessible, since sampling results in minimal patient discomfort and since obtained values reflect the concentrations of drug in the bloodstream. Concentrations in the blood may not be identical to concentrations at the site of action, such as a receptor, but one hopes they serve as a surro-gate that correlates in a proportional manner.

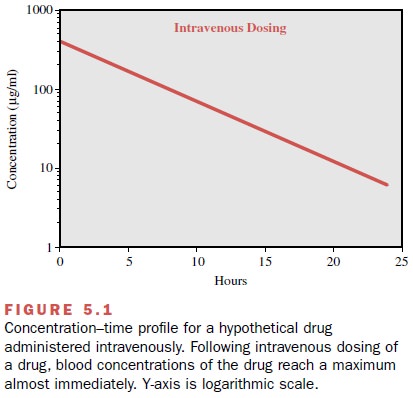
Figure 5.1 shows that for a drug given intravenously, maximum concentrations are achieved almost instanta-neously, since absorption across membranes is not re-quired, though distributive processes may also occur (not depicted for the sake of simplicity). The concentra-tions of drug in the blood decline over time according to the elimination rate of that particular drug. More com-monly, drug is given via extravascular routes (e.g., orally), so absorption and distribution must occur, and therefore it will take some time before maximum con-centrations are achieved.

The blood concentration–time profile for a theoret-ical drug given extravascularly (e.g., orally) is shown in Figure 5.2. Some pharmacokinetic parameters, such as C_max , T_max , area under the curve, and half-life, can be es-timated by visual inspection or computation from a concentration–time profile. 

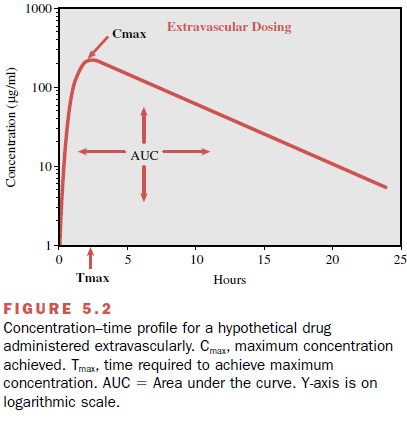
C_max is defined as the maximum concentration achieved in the blood. In Figure 5.2, C_max can be estimated to be approximately 225  μg/mL. The other pharmacokinetic parameter that can be easily es-timated from a concentration–time profile is T_max, or the time needed to reach maximum concentration. In Figure 5.2, the T_max is estimated by visual inspection to be approximately 2 hours. The same drug in a formula-tion that permits a faster rate of absorption would have a shorter T_max and generally a higher C_max than the for-mulation with slower absorptive properties. Likewise, all other things being equal, a drug with a slower elimination rate will generally exhibit a longer Tmax and higher Cmax. 

Once administered, a drug begins undergo-ing absorption, distribution, metabolism, and excretion all at once, not in a sequential fashion, such that all of these processes are involved in determining the shape of a concentration–time profile.

One indicator of the overall exposure of a person to a drug is through the calculation of the area under the curve (AUC). As the name implies, AUC is the mathe-matically integrated area under the concentration–time curve and is most commonly calculated using the trape-zoidal rule of mathematics. In Figure 5.2, the AUC is represented by the shaded area. Though the shape of the concentration–time profile may affect the AUC for a drug, two drugs with entirely different concentra-tion–time profile shapes may have the same AUC. It is, in fact, this property that makes calculating the AUC useful, because it can be used to assess the person’s overall exposure to a drug, even though the individual may have reached different T_max and C_max values from those of other individuals. Furthermore, as will be dis-cussed shortly, AUC is also useful for calculating an-other pharmacokinetic parameter, clearance.

An additional parameter that can be determined from a concentration–time profile is the half-life of the drug, that is, the time it takes for half of the drug to be eliminated from the body. Half-life determination is very useful, since it can readily be used to evaluate how long a drug is expected to remain in the body after ter-mination of dosing, the time required for a drug to reach steady state (when the rate of drug entering the body is equal to the rate of drug leaving the body), and often the frequency of dosing. The following equation is used to calculate the half-life of a drug:

t_1/2 = 0.693/ k_e

where t_1/2 is the half-life and k_e is the elimination rate constant calculated from the slope of the declining por-tion of the concentration–time profile (Fig. 5.3). By def-inition, half-life denotes that 50% of the drug in the body at a given time will be eliminated over the calcu-lated period. However, this does not mean that the same amount of drug is eliminated each half-life. For ex-ample, Figure 5.3 shows that during the first half-life pe-riod (0–5 hours) the drug concentration is reduced from 100 μg/mL to 50 μg/mL. However, during the second half-life period (5–10 hours), even though the amount in the body is reduced by 50%, the concentration falls only from 50 μg/mL to 25 μg/mL (a reduction in con-centration of 25 μg/mL). This concept is also illustrated in Table 5.1. It takes approximately five half-lives for 97% of the drug to be eliminated from the body (re-gardless of the duration of the half-life). 

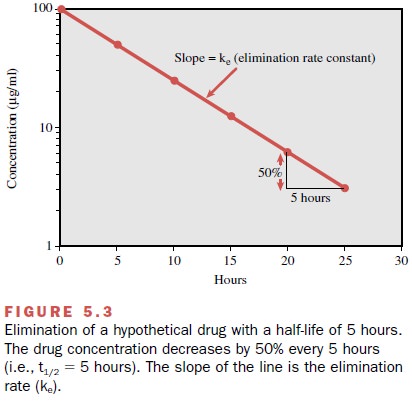
Thus, if one wished to switch a patient from one drug to another but not have both drugs present in substantial quantities, the clinician must wait five half-lives (in this case, 25 hours) before administering the second drug. It will also require five half-lives for a drug to reach steady state, again, independent of the duration of the half-life. Steady state is when the amount of drug entering the body is equal to the amount of drug being eliminated in a given period. Finally, it is a rule of thumb (though certainly not ab-solute) that drugs are generally dosed every half-life (with allowance for rounding to convenient intervals). Thus, the concept of half-life has considerable impor-tance for determining dosing frequency or adjusting doses in a patient.